What Is Square Root Of 125
Juapaving
Apr 05, 2025 · 5 min read
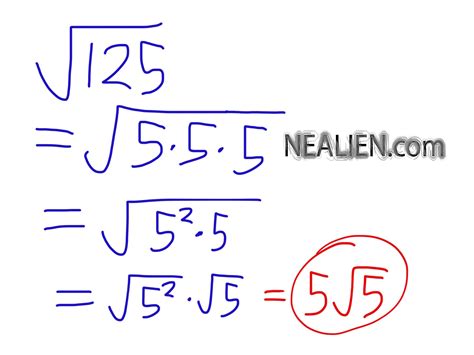
Table of Contents
What is the Square Root of 125? A Deep Dive into Square Roots and Simplification
The question, "What is the square root of 125?" might seem simple at first glance. However, understanding the answer fully involves delving into the concepts of square roots, prime factorization, and simplifying radicals. This comprehensive guide will not only provide the answer but also equip you with the knowledge to tackle similar problems with confidence.
Understanding Square Roots
Before we tackle the square root of 125, let's refresh our understanding of what a square root actually is. The square root of a number is a value that, when multiplied by itself, equals the original number. For example, the square root of 9 is 3 because 3 x 3 = 9. We denote the square root using the radical symbol (√).
Key Concepts:
- Perfect Squares: These are numbers that result from squaring an integer (e.g., 4, 9, 16, 25, etc.). Finding the square root of a perfect square is straightforward.
- Non-Perfect Squares: These are numbers that are not the result of squaring an integer (e.g., 125, 7, 10, etc.). Finding the square root of these often involves simplification.
- Principal Square Root: For every positive number, there are two square roots—one positive and one negative. The principal square root is the non-negative square root. For example, while both 3 and -3 squared equal 9, the principal square root of 9 is 3.
Calculating the Square Root of 125: A Step-by-Step Approach
-
Prime Factorization: The first step in simplifying the square root of a non-perfect square is to find its prime factorization. This involves breaking down the number into its prime factors (numbers divisible only by 1 and themselves).
125 can be factored as follows:
125 = 5 x 25 = 5 x 5 x 5 = 5³
-
Simplifying the Radical: Now that we have the prime factorization (5³), we can simplify the square root. Remember that √(a x b) = √a x √b. We look for pairs of identical factors within the prime factorization. Each pair can be brought out from under the radical sign.
√125 = √(5³)= √(5² x 5) = √5² x √5 = 5√5
Therefore, the simplified square root of 125 is 5√5.
Understanding the Result: 5√5
The result, 5√5, is an exact value. It's a combination of a whole number (5) and a radical (√5). It represents an irrational number—a number that cannot be expressed as a simple fraction and its decimal representation goes on forever without repeating.
Let's compare this to an approximate decimal value. The square root of 5 is approximately 2.236. Therefore:
5√5 ≈ 5 x 2.236 ≈ 11.18
So, while 11.18 is an approximation, 5√5 is the precise and simplified form of the square root of 125.
Practical Applications and Further Exploration
Understanding square roots is crucial in various fields, including:
- Geometry: Calculating the lengths of sides in right-angled triangles using the Pythagorean theorem (a² + b² = c²).
- Physics: Solving problems related to velocity, acceleration, and energy.
- Engineering: Designing structures and calculating forces.
- Mathematics: Solving quadratic equations and working with complex numbers.
Expanding on Square Root Concepts
Let's delve deeper into related concepts to solidify our understanding:
Higher-Order Roots
Square roots are a specific type of root (the second root). We can also have cube roots (third root), fourth roots, and so on. The nth root of a number x is a value that, when multiplied by itself n times, equals x.
For example:
- The cube root of 8 (∛8) is 2 because 2 x 2 x 2 = 8.
- The fourth root of 16 (∜16) is 2 because 2 x 2 x 2 x 2 = 16.
Rationalizing the Denominator
In some calculations, you might encounter a radical in the denominator of a fraction. This is often considered undesirable, so we rationalize the denominator by multiplying the numerator and denominator by a suitable expression to eliminate the radical from the denominator.
For example, to rationalize 1/√5, we multiply the numerator and denominator by √5:
(1/√5) x (√5/√5) = √5/5
Operations with Radicals
Radicals can be added, subtracted, multiplied, and divided, but only if they have the same radicand (the number under the radical sign).
- Addition/Subtraction: 2√5 + 3√5 = 5√5
- Multiplication: (√5)(√5) = √25 = 5
- Division: (√10)/√2 = √(10/2) = √5
Advanced Techniques and Challenges
While simplifying square roots like √125 is relatively straightforward, more complex problems might require additional techniques:
- Nested Radicals: These are radicals within radicals (e.g., √(2 + √3)). Simplifying these often requires clever algebraic manipulations.
- Solving Equations with Radicals: Equations involving radicals require careful handling, often involving squaring both sides of the equation (remember to check for extraneous solutions).
- Approximating Square Roots: When an exact value isn't needed, approximation methods, such as the Babylonian method (a type of iterative method), can be used to find a close decimal approximation.
Conclusion: Mastering the Square Root of 125 and Beyond
The square root of 125, simplified to 5√5, is more than just a numerical result. It's a gateway to understanding fundamental mathematical concepts that have far-reaching applications. By mastering the principles of prime factorization, radical simplification, and operations with radicals, you equip yourself with the tools to confidently tackle a wide range of mathematical problems involving square roots and beyond. The journey to mastering this seemingly simple concept opens doors to a deeper appreciation of mathematics and its power in various fields. Continue exploring, practice regularly, and watch your mathematical abilities flourish.
Latest Posts
Latest Posts
-
Cannot Be Measured Ray Or Line Segment
Apr 06, 2025
-
Suppose You Are Walking Down A Street
Apr 06, 2025
-
How Many Feet Is 114 Inches
Apr 06, 2025
-
How To Factorize A Quadratic Equation
Apr 06, 2025
-
Negative 16 X Greater Or Equal Than Negative 48
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about What Is Square Root Of 125 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
