How To Factorize A Quadratic Equation
Juapaving
Apr 06, 2025 · 6 min read
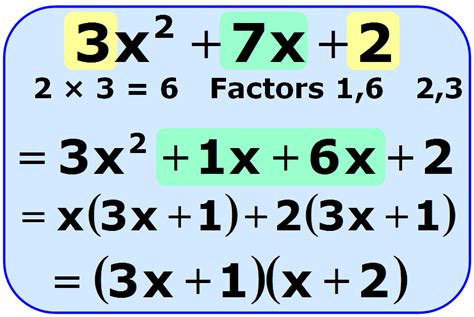
Table of Contents
How to Factorize a Quadratic Equation: A Comprehensive Guide
Quadratic equations are fundamental to algebra and appear frequently in various fields, from physics and engineering to finance and computer science. Understanding how to factorize these equations is crucial for solving them efficiently and extracting meaningful information. This comprehensive guide will explore different methods for factorizing quadratic equations, providing you with a solid foundation to tackle this important mathematical concept.
Understanding Quadratic Equations
Before diving into factorization techniques, let's solidify our understanding of quadratic equations. A quadratic equation is a polynomial equation of the second degree, meaning the highest power of the variable (usually denoted as 'x') is 2. It generally takes the form:
ax² + bx + c = 0
where:
- a, b, and c are constants (numbers), and
- a ≠ 0 (if a were 0, it wouldn't be a quadratic equation).
The solutions to a quadratic equation are the values of x that make the equation true. These solutions are also known as roots, zeros, or x-intercepts.
Methods for Factorizing Quadratic Equations
There are several methods for factorizing quadratic equations. The most common are:
1. Factoring by Inspection (Trial and Error)
This method involves finding two binomials whose product equals the quadratic expression. It's best suited for simpler quadratic equations where the coefficients (a, b, and c) are relatively small.
Steps:
- Identify the factors of 'a' and 'c'. Remember that 'a' is the coefficient of x², and 'c' is the constant term.
- Find pairs of factors that, when added, equal 'b'. 'b' is the coefficient of x.
- Construct the binomial factors. Use the pairs of factors you found to create two binomials in the form (px + q)(rx + s), where p and r are factors of 'a', and q and s are factors of 'c'. The combination should result in the original quadratic equation when expanded.
Example:
Factorize x² + 5x + 6 = 0
- Factors of a (1) are 1 and 1.
- Factors of c (6) are 1 and 6, or 2 and 3.
- The pair (2 and 3) adds up to b (5).
- Therefore, the factorization is (x + 2)(x + 3) = 0.
Advantages: Quick and efficient for simple equations.
Disadvantages: Can be time-consuming and challenging for more complex equations with larger coefficients or when dealing with negative numbers.
2. The AC Method (Grouping)
The AC method is a systematic approach that's particularly helpful when dealing with quadratic equations with larger coefficients.
Steps:
- Find the product of 'a' and 'c' (ac).
- Find two factors of 'ac' that add up to 'b'.
- Rewrite the middle term (bx) as the sum of these two factors.
- Factor by grouping. Group the terms into pairs and factor out the greatest common factor (GCF) from each pair.
- Factor out the common binomial. The remaining expression should be the factorization of the original quadratic equation.
Example:
Factorize 6x² + 11x + 4 = 0
- ac = 6 * 4 = 24
- Factors of 24 that add up to 11 are 3 and 8.
- Rewrite the equation: 6x² + 3x + 8x + 4 = 0
- Factor by grouping: 3x(2x + 1) + 4(2x + 1) = 0
- Factor out the common binomial: (3x + 4)(2x + 1) = 0
Advantages: Works effectively even with larger coefficients.
Disadvantages: More steps involved compared to factoring by inspection.
3. Using the Quadratic Formula
The quadratic formula is a powerful tool that provides the roots of any quadratic equation, regardless of its factorability. While it doesn't directly provide the factorization, it helps find the roots, which can then be used to construct the factors.
The quadratic formula is:
x = [-b ± √(b² - 4ac)] / 2a
Steps:
- Identify a, b, and c.
- Substitute these values into the quadratic formula.
- Solve for x. You will get two solutions (roots), x₁ and x₂.
- Construct the factors. The factors are (x - x₁) and (x - x₂).
Example:
Factorize 2x² - 5x + 2 = 0
- a = 2, b = -5, c = 2
- Substitute into the quadratic formula: x = [5 ± √((-5)² - 4 * 2 * 2)] / (2 * 2) = [5 ± √9] / 4 = [5 ± 3] / 4
- Solutions: x₁ = 2, x₂ = 1/2
- Factors: (x - 2) and (x - 1/2) Therefore, the factored form is (x-2)(2x-1)=0 (Note: we need to adjust the second factor to maintain the original equation)
Advantages: Works for all quadratic equations, including those that are not easily factorizable by inspection or the AC method.
Disadvantages: Requires more calculations than other methods.
4. Difference of Squares
This method applies specifically to quadratic equations of the form:
a²x² - b² = 0
This can be factorized as:
(ax + b)(ax - b) = 0
Example:
Factorize 9x² - 16 = 0
This is a difference of squares where a = 3 and b = 4. The factorization is: (3x + 4)(3x - 4) = 0
Advantages: Simple and quick for this specific type of quadratic equation.
Disadvantages: Only applicable to difference of squares.
Solving Quadratic Equations After Factorization
Once a quadratic equation is factorized, finding its solutions is straightforward. Since the product of the factors is zero, at least one of the factors must be zero. This leads to two separate equations, each solved for x:
Example: (x + 2)(x + 3) = 0
This gives us two equations:
x + 2 = 0 => x = -2 x + 3 = 0 => x = -3
Therefore, the solutions to the quadratic equation x² + 5x + 6 = 0 are x = -2 and x = -3.
Choosing the Right Method
The best method for factorizing a quadratic equation depends on the specific equation and your comfort level with each technique. For simple equations, factoring by inspection is often quickest. For more complex equations, the AC method or the quadratic formula are more reliable. The difference of squares method is a specialized technique for a particular type of quadratic equation. Practice with all methods to develop a strong understanding and efficiency in solving quadratic equations.
Advanced Concepts and Applications
Understanding factorization opens doors to more advanced concepts in algebra. Let's briefly touch upon some of these:
-
Completing the Square: This technique is crucial for deriving the quadratic formula and understanding the geometric interpretation of quadratic equations. It involves manipulating the equation to create a perfect square trinomial, which can then be easily factored.
-
Discriminant: The discriminant (b² - 4ac) from the quadratic formula provides valuable information about the nature of the roots. If the discriminant is positive, there are two distinct real roots; if it's zero, there's one real root (a repeated root); and if it's negative, there are two complex roots (involving imaginary numbers).
-
Parabolas: Quadratic equations represent parabolas graphically. The roots of the equation correspond to the x-intercepts of the parabola. Understanding factorization helps in sketching and analyzing parabolas, crucial in areas like projectile motion and optimization problems.
-
Partial Fraction Decomposition: In calculus, factorization is vital for decomposing rational functions into simpler fractions, simplifying integration problems.
Conclusion
Factorizing quadratic equations is a fundamental skill in algebra with broad applications. By mastering the different methods outlined in this guide – factoring by inspection, the AC method, the quadratic formula, and the difference of squares – you'll be well-equipped to solve a wide range of quadratic equations efficiently and confidently. Remember to practice regularly and choose the method best suited to the problem at hand. This solid foundation will serve you well as you progress to more advanced algebraic concepts and their real-world applications. The key is consistent practice and understanding the underlying principles. Remember to always check your answers by expanding the factored form to ensure it matches the original quadratic equation.
Latest Posts
Latest Posts
-
How Much Is 20 Square Feet
Apr 06, 2025
-
Each Orbital Can Hold How Many Electrons
Apr 06, 2025
-
5 Letter Words Beginning With Thu
Apr 06, 2025
-
Isotopes Of The Same Element Have Different
Apr 06, 2025
-
Least Common Multiple Of 3 4 And 9
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about How To Factorize A Quadratic Equation . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
