Cannot Be Measured Ray Or Line Segment
Juapaving
Apr 06, 2025 · 6 min read
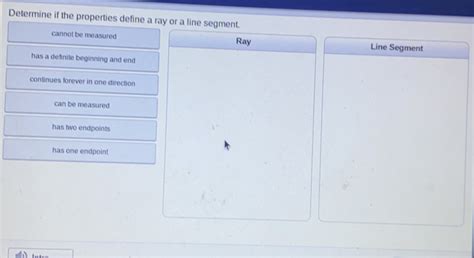
Table of Contents
The Unmeasurable: Exploring the Nature of Rays and Line Segments
The seemingly simple concepts of rays and line segments, fundamental building blocks of geometry, conceal a fascinating paradox: while we can readily visualize and manipulate them, precisely measuring their length in the truest sense presents an insurmountable challenge. This article delves into the nature of rays and line segments, exploring why their measurement, in a complete and absolute sense, remains beyond our grasp.
Understanding Rays and Line Segments: A Geometric Primer
Before venturing into the intricacies of measurement, let's establish a clear understanding of rays and line segments.
Defining a Line Segment
A line segment is a portion of a straight line that's bounded by two distinct endpoints. Think of it as a finite piece of a line, with a definite beginning and a definite end. We can readily represent a line segment using two capital letters, such as AB, where A and B denote the endpoints. The length of a line segment is defined as the distance between these two endpoints. This distance can be measured, at least theoretically, with tools like rulers, although practical limitations always exist at a microscopic level.
Defining a Ray
A ray, on the other hand, is a portion of a line that extends infinitely in one direction from a single endpoint. Imagine a laser beam – it originates from a specific point and continues indefinitely. We typically represent a ray using two capital letters, say AB, where A denotes the starting point (endpoint), and B is any other point on the ray. The arrow over AB indicates its unbounded nature. Unlike a line segment, a ray possesses only one endpoint, extending infinitely in the other direction.
The Challenge of Measurement: Infinity and Precision
The inherent difficulty in measuring rays and line segments stems from the fundamental nature of infinity and the limitations of our measuring tools.
The Impossibility of Measuring a Ray
The concept of measuring a ray presents an immediate hurdle. Because it extends infinitely, any attempt to assign a numerical value to its length is inherently futile. No matter how large a number we choose, the ray stretches beyond it. We can conceptually divide it into segments, but the sum of these segments would still be infinite. Therefore, it is impossible to assign a finite length to a ray. This is not a limitation of our tools, but a fundamental consequence of the ray’s definition.
The Practical Limitations of Measuring a Line Segment
While we can assign a length to a line segment, true, perfect measurement remains elusive. This is not just a technological challenge; it’s a conceptual one.
1. The Atomic Limit: At the atomic and subatomic levels, the concept of a continuous, smooth line breaks down. Matter is composed of discrete particles, and the apparent "continuity" of a line segment is an approximation. Any attempt to measure a line segment with ultimate precision would be restricted by the size of the atoms or the particles making up the ruler and the line segment itself.
2. The Problem of Precision: Even ignoring the atomic limit, achieving perfect precision in measurement is practically impossible. Any physical measurement involves a degree of uncertainty or error. Our tools have limitations in their resolution. A ruler might have millimeter markings, but it cannot measure to the micrometer or nanometer level without additional equipment. Even with advanced instruments, we can only approximate the true length of a line segment; we cannot attain perfect precision.
3. The Role of Definition: The length of a line segment is defined as the distance between two points. But the very notion of "distance" itself relies on a chosen metric and a coordinate system. Changing these would change the measured length. The definition itself introduces a level of abstraction and potential for interpretation.
Exploring the Mathematical Framework: Infinite Series and Limits
To further appreciate the intricacies of this issue, let's examine the mathematical perspectives.
Infinite Series and the Concept of Convergence
Imagine trying to measure a line segment by repeatedly halving its length. Each step creates a new segment half the length of the previous one. This process generates an infinite geometric series:
L + L/2 + L/4 + L/8 + ...
Where 'L' is the initial length of the segment. Mathematically, this series converges to 2L, reflecting the completion of the entire segment. However, we never truly reach the end; the process is conceptually infinite. The convergence simply shows the limit the sum approaches, not that it achieves an absolute value.
Limits and the Concept of Approaching Infinity
The concept of a limit is fundamental in calculus. A limit describes the behavior of a function as its input approaches a certain value, often infinity. We can use limits to understand the concept of approaching the length of a line segment, but never definitively attaining its exact length, especially with the atomic limit and practical measurement errors factored in.
The Paradox of Zeno's Dichotomy
Zeno of Elea's paradoxes, particularly the dichotomy paradox, vividly illustrate this issue. The paradox argues that motion is impossible because to reach a destination, one must first traverse half the distance, then half of the remaining distance, and so on ad infinitum. This never-ending halving process creates an infinite number of steps, seemingly preventing the destination from ever being reached. This relates to the challenge of measuring a line segment, where we can conceptually subdivide it endlessly, delaying the attainment of a precise length.
Practical Implications and Applications
Despite the inherent impossibility of perfect measurement, the concepts of rays and line segments remain indispensable in various fields.
Geometry and Spatial Reasoning
In geometry, rays and line segments serve as fundamental building blocks for constructing shapes and analyzing spatial relationships. While perfect measurement is not always necessary, the concepts are crucial for defining angles, triangles, and other geometric figures. The relative lengths of segments are often more significant than their absolute values.
Computer Graphics and CAD
In computer-aided design (CAD) and computer graphics, line segments are widely used to represent objects and surfaces. While computers deal with finite precision, they can approximate the length of line segments with sufficient accuracy for practical applications. The approximations are accurate enough for the visualizations and calculations required by the software.
Physics and Engineering
In physics and engineering, vectors, often represented by line segments, describe quantities such as force, velocity, and displacement. Again, absolute precision is not always necessary, and the relative magnitudes and directions of these vectors are critical. The mathematical calculations work effectively using approximate values.
Cartography and Mapping
In cartography, line segments and rays help represent roads, boundaries, and other geographic features. While maps are representations rather than exact replicas, they utilize line segments to effectively communicate spatial information with sufficient accuracy for practical purposes.
Conclusion: Embracing the Approximations
The unmeasurable nature of rays and the challenge of perfectly measuring line segments highlight the fascinating interplay between theoretical concepts and practical limitations. While perfect measurement remains elusive, the concepts themselves remain essential tools in various fields. The focus shifts from absolute precision to acceptable approximations that meet the demands of specific applications. Understanding the limitations of measurement helps refine our understanding of geometric concepts and improves the accuracy and efficacy of our practical applications. This journey into the unmeasurable highlights the subtle yet profound limitations of measurement, enriching our understanding of the very fundamentals of geometry.
Latest Posts
Latest Posts
-
How Much Is 20 Square Feet
Apr 06, 2025
-
Each Orbital Can Hold How Many Electrons
Apr 06, 2025
-
5 Letter Words Beginning With Thu
Apr 06, 2025
-
Isotopes Of The Same Element Have Different
Apr 06, 2025
-
Least Common Multiple Of 3 4 And 9
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about Cannot Be Measured Ray Or Line Segment . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
