What Is A Negative Rational Number
Juapaving
Apr 02, 2025 · 6 min read
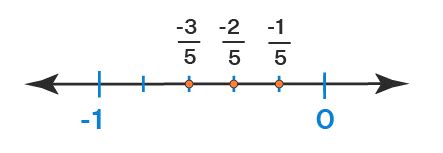
Table of Contents
What is a Negative Rational Number? A Deep Dive into Number Systems
Understanding negative rational numbers is fundamental to grasping the broader landscape of mathematics. This comprehensive guide will explore the definition, properties, representations, and applications of negative rational numbers, ensuring a thorough understanding for both beginners and those seeking a refresher.
Defining Rational Numbers
Before diving into negative rational numbers, let's establish a clear understanding of what constitutes a rational number. A rational number is any number that can be expressed as the quotient or fraction p/q of two integers, where p is the numerator and q is the denominator, and q is not zero (since division by zero is undefined). This seemingly simple definition encompasses a vast range of numbers.
Examples of rational numbers include:
- 1/2: One-half
- 3/4: Three-quarters
- -2/5: Negative two-fifths
- 7: Seven (can be expressed as 7/1)
- 0: Zero (can be expressed as 0/1)
- -10: Negative ten (can be expressed as -10/1)
Introducing Negative Rational Numbers
A negative rational number is simply a rational number that is less than zero. It's a fraction where the numerator and denominator are integers, the denominator is not zero, and the overall value of the fraction is negative. This negativity can arise in several ways:
-
Negative numerator, positive denominator: For example, -3/4, -7/2, -11/1. In these cases, a negative number is being divided by a positive number, resulting in a negative quotient.
-
Positive numerator, negative denominator: For example, 3/-4, 7/-2, 11/-1. Here, a positive number is divided by a negative number, again yielding a negative quotient.
-
Both negative numerator and denominator: For example, -3/-4, -7/-2, -11/-1. While both the numerator and denominator are negative, the resulting fraction simplifies to a positive value. This highlights the crucial rule of signs in division: a negative divided by a negative equals a positive.
Therefore, to identify a negative rational number, focus on the overall sign of the fraction after simplification.
Properties of Negative Rational Numbers
Negative rational numbers share many properties with their positive counterparts, but with key distinctions stemming from their negative sign. These properties are crucial for performing mathematical operations:
-
Addition: Adding a negative rational number is equivalent to subtracting its positive counterpart. For example, 1/2 + (-1/4) = 1/2 - 1/4 = 1/4.
-
Subtraction: Subtracting a negative rational number is equivalent to adding its positive counterpart. For example, 1/3 - (-2/3) = 1/3 + 2/3 = 1.
-
Multiplication: Multiplying two negative rational numbers results in a positive rational number. Multiplying a negative rational number by a positive rational number results in a negative rational number. For instance, (-1/2) * (-2/3) = 1/3, and (-1/2) * (2/3) = -1/3.
-
Division: Dividing a negative rational number by a positive rational number results in a negative rational number. Dividing a negative rational number by a negative rational number results in a positive rational number. For instance, (-1/2) / (1/4) = -2, and (-1/2) / (-1/4) = 2.
-
Ordering: Negative rational numbers are always less than zero and less than any positive rational number. They are ordered in a similar way to positive rational numbers, with smaller numerators (relative to denominators) representing smaller values. For instance, -1/2 > -3/4.
-
Density: Like all rational numbers, negative rational numbers are densely packed on the number line. Between any two distinct negative rational numbers, you can always find infinitely many other negative rational numbers.
Representations of Negative Rational Numbers
Negative rational numbers can be represented in various ways:
-
Fraction form: This is the most common representation, explicitly showing the numerator and denominator (e.g., -3/5, -7/2).
-
Decimal form: Converting a fraction to a decimal often results in a terminating or repeating decimal. For instance, -3/5 = -0.6, and -1/3 = -0.333...
-
Percentage form: A negative rational number can also be expressed as a negative percentage. For example, -1/4 = -25%.
Applications of Negative Rational Numbers
Negative rational numbers are ubiquitous in various fields:
-
Finance: Representing debt, losses, deficits, or negative balances in bank accounts.
-
Temperature: Measuring temperatures below zero degrees Celsius or Fahrenheit.
-
Elevation: Representing points below sea level.
-
Physics: Describing velocity in the opposite direction of a chosen reference point (e.g., negative velocity).
-
Coordinate systems: Indicating locations on a coordinate plane with negative coordinates.
-
Computer science: Representing negative indices in arrays or negative values in data structures.
Comparing and Ordering Negative Rational Numbers
Comparing negative rational numbers requires careful attention. Remember that the further a number is to the left of zero on the number line, the smaller its value.
To compare two negative rational numbers:
- Find a common denominator: This makes it easier to compare the numerators.
- Compare the numerators: The fraction with the larger (in absolute value) numerator will be smaller in value.
Example: Compare -2/3 and -5/6.
Find a common denominator (6): -4/6 and -5/6.
Since -5 is smaller than -4, -5/6 < -2/3.
Working with Negative Rational Numbers: Practical Examples
Let's illustrate the practical application of operations with negative rational numbers:
Example 1: Addition
A scuba diver descends 1/2 meter and then descends another 1/4 meter. What is their total depth?
Total depth = -1/2 + (-1/4) = -1/2 - 1/4 = -3/4 meters.
Example 2: Subtraction
The temperature rises from -2°C to 1°C. What is the temperature increase?
Temperature increase = 1°C - (-2°C) = 1°C + 2°C = 3°C.
Example 3: Multiplication
A company loses 1/5 of its profit every quarter. If the profit is 100,000, what is the total loss in two quarters?
Loss per quarter = -1/5 * 100,000 = -20,000 Total loss in two quarters = -20,000 * 2 = -40,000
Negative Rational Numbers and the Number Line
The number line provides a visual representation of rational numbers, including negative rational numbers. Zero is at the center, positive numbers extend to the right, and negative numbers extend to the left. Negative rational numbers are positioned to the left of zero, with their position reflecting their magnitude (the further left, the smaller the value).
Advanced Concepts and Related Topics
The understanding of negative rational numbers forms the foundation for more advanced concepts:
-
Real numbers: Rational numbers, along with irrational numbers (like π and √2), make up the set of real numbers.
-
Complex numbers: These numbers extend beyond the real numbers, incorporating imaginary units (√-1).
-
Inequalities: Working with inequalities involving negative rational numbers requires careful attention to the signs and ordering.
-
Algebra: Negative rational numbers are extensively used in algebraic equations and manipulations.
Conclusion
Negative rational numbers, while seemingly simple, play a critical role in various mathematical applications and real-world scenarios. Mastering their properties, representations, and operations is crucial for success in mathematics and related fields. This comprehensive exploration provided a solid grounding in the subject, enabling you to confidently tackle problems and delve into more advanced mathematical concepts. Remember to practice regularly and apply your knowledge to real-world examples to solidify your understanding.
Latest Posts
Latest Posts
-
How Is Photosynthesis And Cellular Respiration Different
Apr 03, 2025
-
Which Of The Following Is Strongest Acid
Apr 03, 2025
-
Are Prime Numbers Even Or Odd
Apr 03, 2025
-
What Is 104 Degrees Fahrenheit In Celsius
Apr 03, 2025
-
Fossil Fuels Are Classified As Non Renewable Because They
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about What Is A Negative Rational Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
