Are Prime Numbers Even Or Odd
Juapaving
Apr 03, 2025 · 6 min read
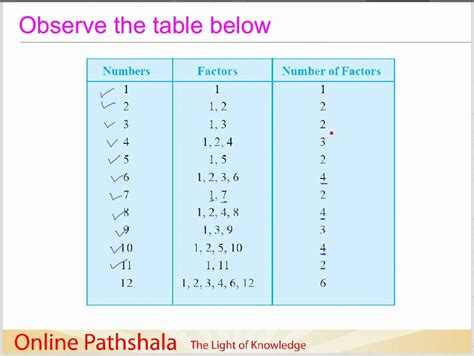
Table of Contents
Are Prime Numbers Even or Odd? A Deep Dive into Number Theory
The question of whether prime numbers are even or odd might seem deceptively simple at first glance. A quick look at the first few primes – 2, 3, 5, 7, 11 – reveals a pattern: most are odd. However, the exception, the number 2, throws a wrench into any simple generalization. This seemingly elementary question opens a door to a fascinating exploration of number theory, prime numbers, and their fundamental properties. This comprehensive article will delve into the intricacies of prime numbers, explaining why the even/odd distinction is crucial and exploring the mathematical reasoning behind the classification.
Understanding Prime Numbers
Before diving into the even/odd debate, let's establish a firm understanding of what constitutes a prime number. A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. This seemingly straightforward definition encapsulates a fundamental concept in mathematics that underlies much of modern cryptography and computer science.
Key Characteristics of Prime Numbers:
- Divisibility: A prime number is only divisible by 1 and itself.
- Natural Numbers: Prime numbers belong to the set of natural numbers (1, 2, 3, 4, ...).
- Infinitude: There are infinitely many prime numbers. This profound fact, proven by Euclid, has significant implications in various mathematical fields.
- Fundamental Theorem of Arithmetic: Every integer greater than 1 can be represented uniquely as a product of prime numbers (ignoring the order of the factors). This theorem highlights the fundamental building block nature of prime numbers in the structure of integers.
The Unique Case of 2: The Only Even Prime Number
The number 2 stands out uniquely among prime numbers. It's the only even prime number. This is because the definition of prime numbers hinges on divisibility. Any even number greater than 2 is divisible by 2, meaning it has a divisor other than 1 and itself, thus violating the prime number definition.
Why is 2 the only even prime?
Consider any even number greater than 2. By definition, it can be expressed as 2 * k, where k is some integer greater than 1. This means it's divisible by 2 and k, thus failing the prime number test. Therefore, 2 holds a unique position in the realm of prime numbers as the sole even representative.
Odd Primes: The Vast Majority
The vast majority of prime numbers are odd. This observation stems directly from the fact that all even numbers greater than 2 are composite (non-prime). As we explore higher numbers, the density of primes decreases, but the predominance of odd primes remains.
Generating Odd Primes:
While there's no simple formula to generate all prime numbers, various algorithms and heuristics focus on finding odd primes. This is because eliminating even numbers (except 2) significantly reduces the search space.
The Sieve of Eratosthenes: A Prime Number Hunting Technique
The Sieve of Eratosthenes is a classic algorithm for finding all prime numbers up to a specified integer. It works by iteratively marking the multiples of each prime number as composite, leaving only the prime numbers unmarked. This algorithm implicitly demonstrates the dominance of odd primes, as even numbers (except 2) are immediately eliminated.
Steps in the Sieve of Eratosthenes:
- Create a list: Start with a list of integers from 2 up to the specified limit.
- Mark 2 as prime: 2 is the first prime number.
- Eliminate multiples of 2: Mark all multiples of 2 as composite (non-prime).
- Find the next unmarked number: Find the smallest unmarked number greater than 2. This is the next prime number.
- Eliminate its multiples: Mark all multiples of this prime number as composite.
- Repeat: Repeat steps 4 and 5 until all numbers are either marked as prime or composite.
The Sieve of Eratosthenes visually reinforces the observation that most prime numbers are odd, as the algorithm efficiently removes even numbers early in the process.
Prime Number Theorem and Distribution
The Prime Number Theorem provides a deep insight into the distribution of prime numbers. It states that the number of primes less than or equal to a given number x is approximately x/ln(x). This approximation doesn't directly address the even/odd distribution, but it helps understand the density of primes across the number line. The theorem implies that the primes become increasingly sparse as we move toward larger numbers, regardless of whether they're even or odd.
Twin Primes and Other Prime Number Patterns
Exploring prime number patterns reveals further aspects of their behavior. Twin primes, which are pairs of prime numbers that differ by 2 (e.g., 3 and 5, 11 and 13), are an interesting area of study. The infinitude of twin primes is a famous unsolved problem in number theory. While there's no definitive proof, extensive computational evidence suggests an abundance of twin primes. Interestingly, most twin primes involve odd numbers.
Other patterns, such as cousin primes (primes differing by 4) and sexy primes (primes differing by 6), also show a clear preference for odd numbers. This reinforces the overwhelmingly odd nature of primes beyond the unique case of 2.
The Significance of the Even/Odd Distinction
The even/odd distinction isn't merely a classification; it's a fundamental property that influences various mathematical properties and algorithms involving prime numbers. The simple divisibility rule for even numbers provides a powerful tool for prime number identification and sieving. Many efficient algorithms for prime factorization and primality testing leverage this distinction.
Cryptography and Prime Numbers:
The security of many modern cryptographic systems relies heavily on prime numbers. RSA cryptography, for instance, utilizes large prime numbers to secure data transmission. The even/odd distinction, although seemingly simple, plays a critical role in the underlying mathematical processes of these systems.
Conclusion: 2 is Unique, Most Primes are Odd
In conclusion, the question of whether prime numbers are even or odd reveals a fundamental truth: 2 is the only even prime number. This exception highlights the uniqueness of 2 within the prime number family. The vast majority of prime numbers are odd, a fact underpinned by the definition of prime numbers and reinforced by observation, algorithms like the Sieve of Eratosthenes, and the Prime Number Theorem. Understanding this even/odd distinction is crucial for anyone delving into the world of number theory, cryptography, or the fascinating realm of prime numbers. The seemingly simple question opens doors to a profound exploration of mathematical structure and its implications. Further research into the distribution and properties of prime numbers continues to be a vibrant area of ongoing mathematical investigation.
Latest Posts
Latest Posts
-
Difference Between And Enzyme And A Hormone
Apr 03, 2025
-
What Is Square Root Of 12
Apr 03, 2025
-
What Is The Hardest Substance In The Body
Apr 03, 2025
-
Do Frying Pans Need A Low Specific Heat Capacity
Apr 03, 2025
-
Electron Configuration For A Neutral Atom Of Manganese
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Are Prime Numbers Even Or Odd . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
