How Is A Square Similar To A Rhombus
Juapaving
Mar 31, 2025 · 6 min read
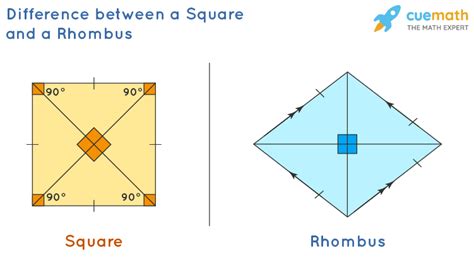
Table of Contents
How is a Square Similar to a Rhombus? Exploring Shared Properties and Key Differences
Squares and rhombuses, both belonging to the fascinating family of quadrilaterals, often cause confusion due to their shared characteristics. While distinct shapes, understanding their similarities and differences is crucial for grasping fundamental geometric concepts. This article delves deep into the properties of squares and rhombuses, highlighting their commonalities and contrasting features. We will explore their sides, angles, diagonals, and area calculations to paint a complete picture of their relationship. By the end, you'll confidently differentiate between these two shapes and appreciate their interconnectedness within the broader context of geometry.
Shared Properties: The Foundation of Similarity
At their core, squares and rhombuses share several key properties, which form the basis of their similarity. These shared characteristics are the building blocks that unite these seemingly distinct shapes. Let's delve into these fundamental similarities:
1. All Sides are Equal: The Defining Feature
The most prominent similarity between a square and a rhombus is that all their sides are of equal length. This fundamental characteristic is the defining feature of both shapes. This means that if you measure the length of each side of a square, you'll find they are identical; the same holds true for a rhombus. This property fundamentally sets them apart from other quadrilaterals like rectangles or parallelograms, which may have sides of varying lengths. This shared trait is visually striking and a cornerstone of their geometrical kinship.
2. Opposite Sides are Parallel: Maintaining Symmetry
Both squares and rhombuses exhibit parallelism in their opposite sides. This means that the sides positioned opposite each other are parallel lines. This characteristic contributes to the overall symmetry of both shapes, ensuring that they maintain a balanced and regular form. This parallel property is important for understanding their behaviour under various transformations and for calculations involving their areas and perimeters.
3. Opposite Angles are Equal: A Symmetrical Arrangement
A further shared feature is the equality of opposite angles. In both squares and rhombuses, the angles positioned opposite each other are equal in measure. This symmetrical arrangement enhances the visual balance and mathematical consistency of both shapes. This property is crucial for understanding their rotational symmetry and for solving problems involving angle calculations within the shapes. The consistency of opposite angles underlines their structural uniformity.
Where They Differ: Unveiling the Distinctive Traits
While the shared properties highlight the similarities, it's crucial to understand where squares and rhombuses diverge. These differences are what truly distinguish a square from a rhombus. Let's examine these differentiating factors:
1. Angles: The Defining Difference
The most significant difference lies in their angles. A square possesses four right angles (90°), making it a special type of rectangle. Each corner of a square forms a perfect 90° angle, creating a highly symmetrical and stable structure. In contrast, a rhombus, while having equal side lengths, doesn't necessarily have right angles. Its angles can vary, with opposite angles being equal but not necessarily 90°. This means a rhombus can be "squished" or distorted, while a square maintains its perfectly square shape. This angle distinction is the critical factor that separates the two shapes definitively.
2. Diagonals: A Tale of Two Behaviours
While both shapes have diagonals that bisect each other, their behaviour differs significantly. In a square, the diagonals are equal in length and intersect at right angles (90°), bisecting each other perfectly. This creates four congruent right-angled triangles within the square. However, in a rhombus, the diagonals are also bisecting each other, but they are not necessarily equal in length, and they intersect at non-right angles. This difference in diagonal behaviour directly reflects the difference in their angle properties, showcasing the impact of angle variation on the overall geometry of the rhombus.
3. Area Calculation: Reflecting Shape Differences
The area calculation reflects the differences in shape. For a square, the area is simply the side length squared (side * side). The formula's simplicity reflects the square's inherent regularity and symmetry. Calculating the area of a rhombus, however, requires considering the lengths of its diagonals. The formula is (1/2) * d1 * d2, where d1 and d2 are the lengths of the two diagonals. This more complex formula highlights the impact of varying angles and diagonal lengths on the rhombus's area. The different area calculation methods mirror the fundamental differences in their geometrical properties.
Visualizing the Relationship: A Hierarchical Perspective
To fully grasp the relationship between squares and rhombuses, it's helpful to visualize them within a hierarchical structure. Think of it like a family tree of quadrilaterals. Parallelograms form the broad category, encompassing shapes with opposite sides parallel. Within parallelograms, we find rhombuses, defined by their equal side lengths. Squares, however, are a specialized subset of both rhombuses and rectangles. This means that all squares are rhombuses (and rectangles), but not all rhombuses are squares. This hierarchical understanding helps to clarify their relationship and avoid misconceptions.
Real-World Applications: Squares and Rhombuses in Action
Understanding the properties of squares and rhombuses is not just an academic exercise; it has practical applications in numerous fields:
-
Architecture and Construction: Squares and rectangles (a close relative of the square) are fundamental in building design, ensuring stability and efficient space utilization. Rhombuses find applications in architectural designs where visual interest and structural support are intertwined.
-
Engineering: The structural integrity of squares and rhombuses is crucial in engineering applications, from bridge designs to lattice structures. Their symmetrical properties allow for efficient load distribution and structural strength.
-
Art and Design: Squares and rhombuses are widely used in artistic creations and graphic design. They provide a visual framework for creating balance, symmetry, and visual impact. Their geometric regularity is appealing in various design styles.
-
Crystallography: The symmetrical shapes of squares and rhombuses are found in the structure of various crystals, reflecting their mathematical properties at a molecular level. Their regular structures provide insight into the underlying organization of crystalline materials.
Conclusion: Appreciating the Interplay of Geometry
Squares and rhombuses, while distinct shapes, share crucial commonalities that bind them within the broader family of quadrilaterals. Their shared properties – equal side lengths, parallel opposite sides, and equal opposite angles – underscore their geometric kinship. However, the differences in their angles and diagonal behaviour clearly distinguish them. Recognizing both the similarities and differences is essential for a deeper understanding of geometry and its applications in diverse fields. By appreciating the interplay of these properties, we gain a richer comprehension of the mathematical elegance and practical utility of these fundamental geometric forms. This understanding extends beyond simple shape recognition to a grasp of underlying principles that govern geometric relationships. This thorough exploration enables confident differentiation between squares and rhombuses, showcasing their individual properties while acknowledging their shared characteristics within the broader context of geometry.
Latest Posts
Latest Posts
-
Sum Of Exterior Angles Of A Quadrilateral
Apr 01, 2025
-
When Heating A Liquid In A Test Tube You Should
Apr 01, 2025
-
How Many Bones Do Shark Have
Apr 01, 2025
-
Least Common Multiple 12 And 18
Apr 01, 2025
-
What Phase Is The Reverse Of Prophase
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about How Is A Square Similar To A Rhombus . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
