Write The Prime Factorization Of 21.
Juapaving
Mar 31, 2025 · 6 min read
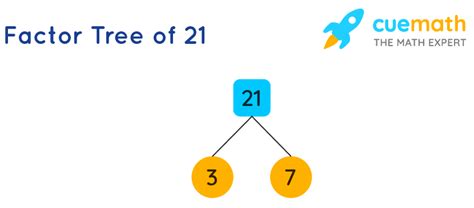
Table of Contents
The Prime Factorization of 21: A Deep Dive into Number Theory
The seemingly simple question, "What is the prime factorization of 21?" opens a door to a fascinating world of number theory. While the answer itself is straightforward, exploring the process and the underlying concepts provides valuable insight into the building blocks of mathematics. This article will not only answer the question but also delve into the significance of prime factorization, its applications, and related mathematical concepts.
Understanding Prime Numbers
Before we tackle the prime factorization of 21, let's solidify our understanding of prime numbers. A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. In simpler terms, it's only divisible by 1 and itself. The first few prime numbers are 2, 3, 5, 7, 11, 13, and so on. 2 is the only even prime number, as all other even numbers are divisible by 2.
Key Characteristics of Prime Numbers:
- Divisibility: A prime number is only divisible by 1 and itself.
- Uniqueness: Every number greater than 1 can be expressed as a unique product of prime numbers (Fundamental Theorem of Arithmetic).
- Infinitude: There are infinitely many prime numbers. This was famously proven by Euclid.
What is Prime Factorization?
Prime factorization, also known as prime decomposition, is the process of finding the prime numbers that, when multiplied together, equal a given number. This process is unique for every number, meaning there's only one way to express a number as a product of primes (ignoring the order of the factors). This uniqueness is a cornerstone of many mathematical theorems and algorithms.
Finding the Prime Factorization of 21
Now, let's get to the main event: finding the prime factorization of 21. We can do this using a simple method:
- Start with the smallest prime number, 2: Is 21 divisible by 2? No, 21 is an odd number.
- Move to the next prime number, 3: Is 21 divisible by 3? Yes, 21 / 3 = 7.
- Continue with the next prime number, 5: Is 7 divisible by 5? No.
- The next prime number is 7: Is 7 divisible by 7? Yes, 7 / 7 = 1.
We've reached 1, meaning we've found all the prime factors. Therefore, the prime factorization of 21 is 3 x 7.
The Fundamental Theorem of Arithmetic
The ability to uniquely factor any number into its prime components is formalized by the Fundamental Theorem of Arithmetic. This theorem states that every integer greater than 1 is either a prime number itself or can be represented as a unique product of prime numbers, up to the order of the factors. This theorem is fundamental to many areas of mathematics, including cryptography and algebra.
Significance of the Fundamental Theorem:
- Uniqueness: The uniqueness aspect is crucial. It means there's only one set of prime numbers that multiply to give a specific composite number. This isn't true for other number systems.
- Building Blocks: Prime numbers act as the fundamental building blocks of all integers. Understanding their factorization reveals the structure and properties of numbers.
- Applications: The theorem has profound implications in various fields, including cryptography (RSA encryption), computational number theory, and abstract algebra.
Methods for Finding Prime Factorization
While the method used for 21 was straightforward, larger numbers require more systematic approaches. Here are some common methods:
1. Factor Tree Method:
This is a visual method, particularly useful for smaller numbers. You start with the number and repeatedly branch off with its prime factors until you reach only prime numbers at the end of each branch.
(Example for 21):
21
/ \
3 7
2. Repeated Division Method:
This involves repeatedly dividing the number by the smallest prime number that divides it evenly. Continue this process until the result is 1.
(Example for 21):
21 / 3 = 7 7 / 7 = 1
Therefore, the prime factors are 3 and 7.
3. Algorithm-Based Methods:
For very large numbers, sophisticated algorithms like the Sieve of Eratosthenes or trial division are employed. These algorithms are optimized for efficiency and speed in factoring large composite numbers.
Applications of Prime Factorization
The seemingly simple process of prime factorization has surprisingly wide-ranging applications in various fields:
1. Cryptography:
The security of many modern cryptographic systems, such as RSA encryption, relies heavily on the difficulty of factoring very large numbers into their prime components. The larger the numbers, the more computationally intensive the factorization becomes, making it practically impossible to break the encryption within a reasonable timeframe.
2. Number Theory:
Prime factorization is a cornerstone of number theory, the branch of mathematics that deals with the properties and relationships of numbers. Many important theorems and concepts in number theory, like the Fundamental Theorem of Arithmetic, rely directly on prime factorization.
3. Computer Science:
Algorithms related to prime factorization are used in various computer science applications, including efficient data structures and algorithms for sorting and searching.
4. Coding Theory:
Prime factorization is crucial in designing error-correcting codes, which are used to ensure reliable data transmission in various communication systems.
Beyond the Basics: Exploring Related Concepts
The exploration of prime factorization opens doors to several related and advanced concepts in mathematics:
1. Greatest Common Divisor (GCD):
The GCD of two or more numbers is the largest number that divides all of them evenly. Prime factorization can be used efficiently to calculate the GCD using the Euclidean algorithm or similar methods.
2. Least Common Multiple (LCM):
The LCM of two or more numbers is the smallest number that is a multiple of all of them. Prime factorization simplifies calculating the LCM as well.
3. Modular Arithmetic:
Modular arithmetic involves operations on remainders after division. Prime numbers play a critical role in modular arithmetic, and understanding prime factorization enhances the understanding of these concepts.
4. Diophantine Equations:
Diophantine equations are algebraic equations where solutions are restricted to integers. Prime factorization often provides valuable insights into solving specific types of Diophantine equations.
Conclusion
The prime factorization of 21, while seemingly trivial at first glance, serves as a gateway to a rich and complex area of mathematics. The Fundamental Theorem of Arithmetic, underpinned by the concept of prime factorization, has profound implications across diverse fields, highlighting the far-reaching impact of this seemingly simple mathematical idea. From the security of online transactions to the efficiency of computer algorithms, the understanding and application of prime factorization remain crucial in our increasingly digital world. The exploration of prime numbers and their factorization continues to captivate mathematicians and computer scientists alike, pushing the boundaries of our understanding of numbers and computation.
Latest Posts
Latest Posts
-
A Tetrad Is Made Up Of
Apr 02, 2025
-
What Is A Single Celled Organism
Apr 02, 2025
-
If Diagonals Of A Quadrilateral Bisect Each Other
Apr 02, 2025
-
Is Pure Water A Mixture Or Compound
Apr 02, 2025
-
What Type Of Device Is A Keyboard
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Write The Prime Factorization Of 21. . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
