A Real Gas Behaves Most Like An Ideal Gas At
Juapaving
Mar 31, 2025 · 5 min read
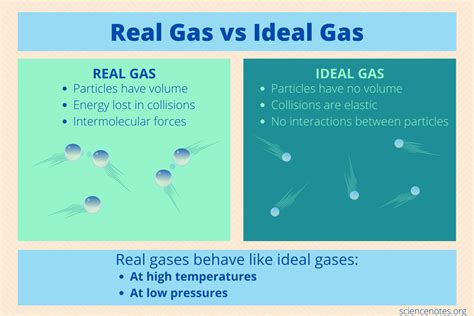
Table of Contents
A Real Gas Behaves Most Like an Ideal Gas At… Low Pressure and High Temperature
Understanding the behavior of gases is crucial in various fields, from chemical engineering to atmospheric science. While the ideal gas law provides a simplified model, real gases deviate from this ideal behavior under certain conditions. This article delves deep into the conditions under which a real gas exhibits characteristics closest to an ideal gas, exploring the underlying principles and the factors that influence deviations.
The Ideal Gas Law: A Foundation for Understanding
The ideal gas law, PV = nRT, elegantly describes the relationship between pressure (P), volume (V), number of moles (n), temperature (T), and the ideal gas constant (R). It assumes that gas particles are point masses with negligible volume and that there are no intermolecular forces between them. These assumptions hold true only under specific conditions.
Limitations of the Ideal Gas Law
Real gases, unlike their ideal counterparts, occupy a finite volume and experience intermolecular forces—attractive (van der Waals forces) and repulsive forces. These forces become significant at high pressures and low temperatures, causing deviations from the ideal gas law.
-
High Pressure: At high pressures, gas molecules are squeezed closer together, and their own volume becomes a significant fraction of the total volume. This contrasts with the ideal gas law's assumption of negligible molecular volume.
-
Low Temperature: At low temperatures, the kinetic energy of gas molecules is reduced, allowing intermolecular attractive forces to dominate. These forces cause the molecules to clump together, reducing the pressure exerted on the container walls compared to what the ideal gas law would predict.
The Conditions for Ideal Gas Behavior in Real Gases
A real gas behaves most like an ideal gas at low pressures and high temperatures. Let's break down why:
1. Low Pressure: Minimizing Molecular Volume and Intermolecular Forces
At low pressures, the gas molecules are widely dispersed. Their individual volumes become insignificant compared to the total volume of the container. This closely resembles the ideal gas assumption of negligible molecular volume. Additionally, the distance between molecules is large, greatly reducing the influence of intermolecular forces. The attractive forces, which would otherwise cause the molecules to clump together and exert less pressure, become negligible.
Example: Imagine a basketball filled with a small number of ping pong balls (representing gas molecules). At low pressure (fewer ping pong balls), the individual volume of each ping pong ball is insignificant compared to the overall volume of the basketball. The ping pong balls are far apart and interactions between them are minimal.
2. High Temperature: Overcoming Intermolecular Forces
At high temperatures, the kinetic energy of the gas molecules is significantly greater than the potential energy due to intermolecular forces. This high kinetic energy allows the molecules to overcome the attractive forces, ensuring they remain largely independent and move randomly. The effect of intermolecular forces on the overall pressure becomes minimal, aligning with the ideal gas assumption of negligible intermolecular forces.
Example: Continuing the basketball analogy, increasing the temperature (giving more kinetic energy to the ping pong balls) allows them to move more rapidly and energetically. This counteracts any tendency for the ping pong balls to cluster together due to weak attractive forces.
Quantifying Deviations: The Compressibility Factor
The compressibility factor (Z) provides a quantitative measure of how much a real gas deviates from ideal behavior. It's defined as:
Z = PV/nRT
For an ideal gas, Z = 1. For real gases:
-
Z > 1: Indicates repulsive forces dominate, leading to a higher pressure than predicted by the ideal gas law. This usually occurs at high pressures.
-
Z < 1: Indicates attractive forces dominate, leading to a lower pressure than predicted by the ideal gas law. This usually occurs at low temperatures.
Real Gas Equations of State: Beyond the Ideal Gas Law
Several equations of state have been developed to better describe the behavior of real gases, accounting for molecular volume and intermolecular forces. The most famous is the van der Waals equation:
(P + a(n/V)²)(V - nb) = nRT
Where:
- 'a' accounts for the attractive intermolecular forces.
- 'b' accounts for the volume occupied by the gas molecules.
Other notable equations of state include the Redlich-Kwong equation, the Peng-Robinson equation, and the virial equation. These equations provide more accurate predictions of real gas behavior, particularly under conditions where the ideal gas law fails.
Applications and Significance
Understanding the conditions under which a real gas behaves ideally is critical in many applications:
-
Chemical Engineering: Designing and optimizing chemical processes often requires accurate predictions of gas behavior. Knowing when the ideal gas law is a valid approximation simplifies calculations significantly.
-
Environmental Science: Modeling atmospheric processes, such as pollutant dispersion and climate change, relies on accurate representations of gas behavior under various conditions.
-
Thermodynamics: Understanding real gas behavior is essential for calculating thermodynamic properties like enthalpy and entropy.
-
Fluid Mechanics: Many fluid mechanics calculations assume ideal gas behavior, but knowing the limits of this assumption is crucial for accurate modeling.
Conclusion
While the ideal gas law offers a simple and useful approximation, real gases deviate from ideal behavior under certain conditions. A real gas behaves most like an ideal gas at low pressures and high temperatures. Under these conditions, the volume occupied by the gas molecules and intermolecular forces become negligible compared to the kinetic energy of the molecules. The compressibility factor, Z, serves as a quantitative measure of the deviation from ideal behavior. More sophisticated equations of state, such as the van der Waals equation, provide more accurate predictions for real gases under various conditions, which is crucial in numerous scientific and engineering applications. Understanding these deviations and applying appropriate equations of state are critical for accurate modeling and prediction in various fields. The principles explored here provide a foundational understanding of gas behavior and its applications in diverse areas of science and engineering. Further investigation into specific equations of state and their applicability under varying conditions will provide a deeper understanding of real gas behavior. This knowledge is essential for scientists, engineers, and anyone involved in applications dealing with gases under diverse conditions. The interplay between pressure, temperature, and the characteristics of real gases is a complex but crucial aspect of numerous scientific and engineering disciplines.
Latest Posts
Latest Posts
-
If Qt Is Perpendicular To Pr
Apr 02, 2025
-
Which Base Is Not Present In Rna
Apr 02, 2025
-
What Is The Lcm Of 5 And 10
Apr 02, 2025
-
Air Moves From High To Low Pressure
Apr 02, 2025
-
The Smallest Particle Of An Element Is A N
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about A Real Gas Behaves Most Like An Ideal Gas At . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
