Name A Pair Of Adjacent Supplementary Angles
Juapaving
Mar 28, 2025 · 6 min read
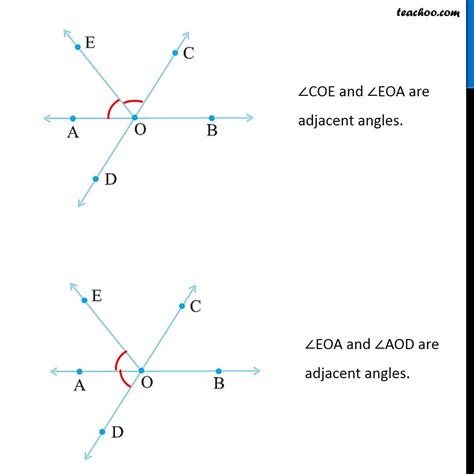
Table of Contents
Naming a Pair of Adjacent Supplementary Angles: A Deep Dive into Geometry
Understanding supplementary angles is fundamental to grasping many geometric concepts. This article delves into the definition of supplementary angles, particularly adjacent supplementary angles, providing clear explanations, real-world examples, and problem-solving techniques. We'll explore various ways to identify and name these angle pairs, ensuring you gain a solid grasp of this essential geometric relationship.
What are Supplementary Angles?
Supplementary angles are two angles whose measures add up to 180 degrees. It's crucial to remember that they don't need to be adjacent (meaning next to each other). They simply need to satisfy the sum condition. For example, a 100° angle and an 80° angle are supplementary because 100° + 80° = 180°.
Key Characteristics of Supplementary Angles:
- Sum of 180°: This is the defining characteristic. If the sum of two angles isn't 180°, they are not supplementary.
- Not Necessarily Adjacent: While they can be adjacent, they don't have to be. This differentiates them from other angle relationships.
- Linear Pairs: A special case of supplementary angles is a linear pair. A linear pair are two adjacent angles that form a straight line. They are always supplementary. This is because a straight line represents an angle of 180°.
Adjacent Supplementary Angles: The Definition and Significance
Adjacent supplementary angles are a specific type of supplementary angle pair. They meet two conditions:
- They are supplementary: Their measures add up to 180°.
- They are adjacent: They share a common vertex (corner) and a common side (ray). They lie next to each other, sharing a boundary.
Visualizing Adjacent Supplementary Angles:
Imagine a straight line. Now, draw a ray starting from a point on that line, but not extending along the line itself. This ray creates two angles that are adjacent and supplementary. They are adjacent because they share the same vertex and a common side. They are supplementary because they together form a straight line, which always measures 180°.
Naming Adjacent Supplementary Angles: A Step-by-Step Guide
Naming angles usually involves using letters to represent points on the rays that form the angles. Let's explore different scenarios and naming conventions.
Scenario 1: Simple Linear Pair
Consider a straight line with a ray drawn from a point on it. Let's label the points A, B, and C, where B is the point on the line and the ray is BC. The two adjacent supplementary angles are then:
- ∠ABC: (Angle ABC) This is one angle formed by the line AB and ray BC.
- ∠CBA: (Angle CBA) – While technically the same angle as ∠ABC, this notation is sometimes used. This is because the middle point represents the vertex, and the order is important only when calculating vectors.
- ∠DBC (Angle DBC) where D is another point on the line extending AB.
Together, ∠ABC and ∠DBC (or ∠ABC and ∠ABD where D is a point beyond B, on the line AB extended) form a linear pair, making them adjacent supplementary angles.
Scenario 2: More Complex Configurations
When dealing with more complex diagrams, the naming convention remains consistent. The key is to identify the common vertex and the common ray that defines the adjacency.
For example, consider two intersecting lines. This creates four angles. Two pairs of these angles are vertically opposite, and two pairs are adjacent supplementary angles. You would name these angles using the points where the lines intersect and the points on the lines themselves. For instance, if the intersection is point O, and points on the lines are A, B, C, and D, you might have angles like ∠AOB, ∠BOC, ∠COD, and ∠DOA. Adjacent supplementary angle pairs would be ∠AOB and ∠BOC, ∠BOC and ∠COD, and so on.
Scenario 3: Using Numbered Angles
Sometimes, angles are labeled with numbers instead of letters. This simplifies the naming process. If you have angles labeled as Angle 1 and Angle 2, and they are adjacent and supplementary, you simply refer to them as Angle 1 and Angle 2.
Real-World Applications of Adjacent Supplementary Angles
Adjacent supplementary angles are not just theoretical concepts; they appear extensively in the real world.
- Construction and Architecture: Architects and engineers frequently use supplementary angles when designing structures. For instance, the angles formed by intersecting walls or beams often represent adjacent supplementary angles. Accurate angle measurements are critical for structural integrity.
- Navigation: In navigation, understanding angle relationships is vital. Pilots and sailors use angles to determine bearings and directions, and the concept of supplementary angles helps in calculating complementary angles which are needed for navigation.
- Graphic Design and Art: Graphic designers utilize supplementary angles when creating symmetrical designs and patterns. The balance and harmony of a design often depend on precise angle measurements.
- Everyday Objects: Many everyday objects feature adjacent supplementary angles. Think about the corners of a door, window, or picture frame. The angles formed at the corners are typically adjacent supplementary angles, all measuring 180 degrees.
Problem-Solving with Adjacent Supplementary Angles
Let's work through some example problems to solidify your understanding.
Problem 1:
Two adjacent angles, ∠X and ∠Y, are supplementary. If the measure of ∠X is 75°, what is the measure of ∠Y?
Solution:
Since ∠X and ∠Y are supplementary, their measures add up to 180°. Therefore:
∠X + ∠Y = 180°
75° + ∠Y = 180°
∠Y = 180° - 75°
∠Y = 105°
Therefore, the measure of ∠Y is 105°.
Problem 2:
Two adjacent angles are supplementary. One angle is twice the size of the other. Find the measure of each angle.
Solution:
Let's call the angles x and 2x. Since they are supplementary:
x + 2x = 180°
3x = 180°
x = 60°
Therefore, one angle measures 60°, and the other measures 2 * 60° = 120°.
Problem 3:
In the figure, lines AB and CD intersect at point E. ∠AE C is 40°. Find the measures of ∠BEC, ∠AED, and ∠DEB.
Solution:
- ∠BEC: ∠AEC and ∠BEC are adjacent supplementary angles, so ∠BEC = 180° - 40° = 140°.
- ∠AED: ∠AEC and ∠AED are vertically opposite angles, so ∠AED = 40°.
- ∠DEB: ∠BEC and ∠DEB are vertically opposite angles, so ∠DEB = 140°.
Conclusion: Mastering Adjacent Supplementary Angles
Understanding adjacent supplementary angles is a fundamental skill in geometry. By grasping their definition, characteristics, naming conventions, and real-world applications, you'll enhance your problem-solving abilities in various mathematical and practical contexts. The ability to identify and work with adjacent supplementary angles will prove invaluable as you progress through more advanced geometric concepts. Practice regularly, and you’ll master this important geometric relationship. Remember to always carefully label your diagrams and use consistent notation for clear and accurate communication.
Latest Posts
Latest Posts
-
Why Is Cellulose Not A Source Of Nutrients For Humans
Mar 30, 2025
-
Law Of Conservation Of Mass States That
Mar 30, 2025
-
Simplify The Square Root Of 12
Mar 30, 2025
-
Find The Area Under The Curve Over The Interval
Mar 30, 2025
-
What Percent Is Equal To 3 8
Mar 30, 2025
Related Post
Thank you for visiting our website which covers about Name A Pair Of Adjacent Supplementary Angles . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
