What Percent Is Equal To 3/8
Juapaving
Mar 30, 2025 · 5 min read
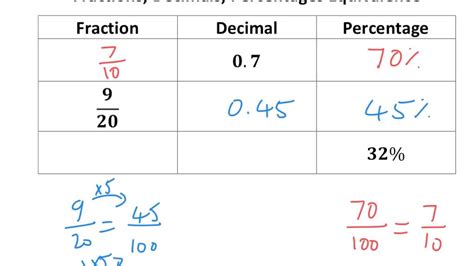
Table of Contents
What Percent is Equal to 3/8? A Comprehensive Guide to Fraction-to-Percentage Conversion
Understanding fractions and percentages is fundamental to various aspects of life, from baking and cooking to finance and data analysis. Knowing how to convert between these two representations is a crucial skill. This comprehensive guide delves into the conversion of the fraction 3/8 into a percentage, explaining the process in detail and exploring related concepts to solidify your understanding. We'll also look at practical applications and provide you with methods to tackle similar conversions independently.
Understanding Fractions and Percentages
Before we dive into the specific conversion of 3/8, let's briefly refresh our understanding of fractions and percentages.
Fractions: A fraction represents a part of a whole. It's composed of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates the number of parts we have, while the denominator indicates the total number of equal parts the whole is divided into. For example, in the fraction 3/8, 3 is the numerator and 8 is the denominator. This means we have 3 out of 8 equal parts.
Percentages: A percentage represents a fraction of 100. The symbol "%" denotes percentage. Essentially, a percentage expresses a proportion relative to 100. For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Converting 3/8 to a Percentage: The Step-by-Step Process
The conversion of a fraction to a percentage involves two main steps:
Step 1: Convert the fraction to a decimal.
To convert a fraction to a decimal, we simply divide the numerator by the denominator. In this case:
3 ÷ 8 = 0.375
Step 2: Convert the decimal to a percentage.
To convert a decimal to a percentage, we multiply the decimal by 100 and add the "%" symbol.
0.375 x 100 = 37.5%
Therefore, 3/8 is equal to 37.5%.
Alternative Methods for Conversion
While the above method is straightforward, there are other approaches you can use to convert fractions to percentages.
Method 1: Using Equivalent Fractions
We can convert 3/8 to an equivalent fraction with a denominator of 100. This involves finding a number that, when multiplied by 8, results in 100. While this isn't always perfectly achievable (as 100 isn't divisible by 8), we can still get a close approximation or use a calculator. The closest we can get is:
- Multiplying both the numerator and denominator by 12.5 gives us (3 x 12.5) / (8 x 12.5) = 37.5/100. This directly translates to 37.5%.
This method illustrates the fundamental principle that equivalent fractions represent the same proportion.
Method 2: Using Proportions
We can set up a proportion to solve for the percentage:
3/8 = x/100
To solve for x, we cross-multiply:
8x = 300
x = 300 ÷ 8 = 37.5
Therefore, x = 37.5%, confirming our previous result.
Practical Applications of Fraction-to-Percentage Conversion
The ability to convert fractions to percentages is essential in many real-world scenarios:
-
Finance: Calculating interest rates, discounts, profit margins, and tax rates often involves converting fractions to percentages. For example, if a bank offers a loan with an interest rate of 3/8, understanding that this is equivalent to 37.5% allows for better financial decision-making.
-
Data Analysis: Representing data in percentage form makes it easier to understand and compare. For instance, if 3 out of 8 students in a class passed an exam, this can be expressed as 37.5% pass rate.
-
Cooking and Baking: Recipes often use fractions to express ingredient quantities. Converting these fractions to percentages can facilitate adjustments for larger or smaller batches.
-
Probability and Statistics: Probability is frequently expressed as a fraction. Converting this to a percentage provides a more intuitive understanding of the likelihood of an event occurring. For example, a 3/8 probability becomes a 37.5% chance.
-
Sales and Marketing: Discount percentages are commonly used to attract customers. Knowing the conversion between fractions and percentages helps in understanding and applying discounts effectively.
Beyond 3/8: Mastering Fraction-to-Percentage Conversions
The methods outlined above are applicable to converting any fraction to a percentage. Let's consider a few more examples:
- 1/4: 1 ÷ 4 = 0.25; 0.25 x 100 = 25%
- 2/5: 2 ÷ 5 = 0.4; 0.4 x 100 = 40%
- 5/6: 5 ÷ 6 ≈ 0.833; 0.833 x 100 ≈ 83.3%
Remember, the key steps are always the same: divide the numerator by the denominator to get a decimal, then multiply the decimal by 100 to obtain the percentage. Rounding may be necessary depending on the desired level of precision.
Troubleshooting Common Mistakes
While fraction-to-percentage conversion is relatively straightforward, some common mistakes can occur:
-
Incorrect Division: Ensure you're dividing the numerator by the denominator, not the other way around.
-
Forgetting to Multiply by 100: Don't forget this crucial step in converting the decimal to a percentage.
-
Rounding Errors: Be mindful of rounding and maintain consistency in the number of decimal places.
-
Using Improper Fractions: Make sure you have a proper fraction (numerator < denominator) before converting. An improper fraction (numerator ≥ denominator) needs to be converted to a mixed number or a whole number plus a fraction before converting to a percentage.
Conclusion: Embracing the Power of Percentage Conversions
Understanding how to convert fractions to percentages is a valuable skill with broad applicability. Mastering this conversion enhances your ability to interpret data, make informed decisions, and communicate effectively across various contexts. By following the steps outlined in this guide and practicing regularly, you can confidently navigate fraction-to-percentage conversions and apply this knowledge to diverse real-world situations. Remember to utilize the various methods discussed to find the approach that best suits your needs and understanding. Consistent practice and attention to detail will solidify your skills and help you avoid common errors, enabling you to confidently work with percentages and fractions in any scenario.
Latest Posts
Latest Posts
-
A Rectangle Is A Square Always Sometimes Never
Apr 01, 2025
-
What Are The First 5 Multiples Of 2
Apr 01, 2025
-
What Is The Numeral For 42
Apr 01, 2025
-
Butter Melting Is A Physical Change
Apr 01, 2025
-
Lowest Common Multiple Of 20 And 8
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is Equal To 3/8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
