Simplify The Square Root Of 12
Juapaving
Mar 30, 2025 · 4 min read
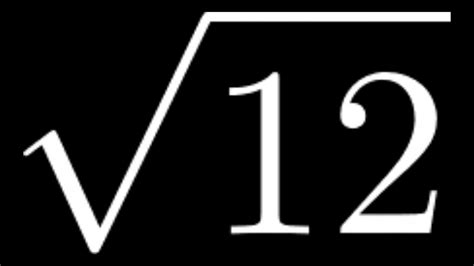
Table of Contents
- Simplify The Square Root Of 12
- Table of Contents
- Simplifying the Square Root of 12: A Comprehensive Guide
- Understanding Square Roots and Prime Factorization
- Simplifying √12: The Step-by-Step Process
- Why Simplifying Square Roots Matters
- Common Mistakes to Avoid
- Advanced Examples of Square Root Simplification
- Practical Applications and Further Exploration
- Latest Posts
- Latest Posts
- Related Post
Simplifying the Square Root of 12: A Comprehensive Guide
Simplifying square roots is a fundamental concept in mathematics, crucial for various applications from algebra to calculus. This comprehensive guide will delve into the process of simplifying the square root of 12, explaining the underlying principles and providing numerous examples to solidify your understanding. We'll explore different methods, address common misconceptions, and equip you with the skills to tackle similar problems with confidence.
Understanding Square Roots and Prime Factorization
Before jumping into simplifying √12, let's refresh our understanding of square roots and prime factorization. A square root of a number is a value that, when multiplied by itself, gives the original number. For instance, the square root of 9 (√9) is 3 because 3 x 3 = 9.
Prime factorization is the process of breaking down a number into its prime factors – numbers divisible only by 1 and themselves. This is the cornerstone of simplifying square roots. Prime numbers less than 20 include 2, 3, 5, 7, 11, 13, 17, and 19. Every composite number can be expressed as a unique product of primes.
Simplifying √12: The Step-by-Step Process
The simplification of √12 relies heavily on prime factorization. Here's a step-by-step guide:
-
Find the Prime Factorization of 12: We break down 12 into its prime factors:
12 = 2 x 6 = 2 x 2 x 3 = 2² x 3
-
Rewrite the Square Root: Now, rewrite the square root of 12 using the prime factorization:
√12 = √(2² x 3)
-
Separate the Factors: Because the square root of a product is the product of the square roots, we can separate the factors:
√(2² x 3) = √2² x √3
-
Simplify the Perfect Square: The term √2² simplifies to 2 because 2 x 2 = 2².
2 x √3
-
Final Simplified Form: Therefore, the simplified form of √12 is 2√3.
Why Simplifying Square Roots Matters
Simplifying square roots isn't just an exercise in mathematics; it has practical applications in various fields:
-
Algebra: Simplifying radicals often streamlines algebraic expressions, making them easier to manipulate and solve equations. For example, when solving quadratic equations, simplified radicals lead to cleaner and more manageable solutions.
-
Geometry: Calculations involving areas, volumes, and lengths frequently involve square roots. Simplifying radicals ensures precision and efficiency in geometric computations. Consider calculating the diagonal of a rectangle – often, the result involves a square root that needs simplification.
-
Trigonometry: Trigonometric functions and their inverses often yield results involving square roots, requiring simplification for accurate calculations and interpretation.
-
Calculus: Derivatives and integrals often involve simplifying square roots to handle complex expressions more easily.
Common Mistakes to Avoid
Several common mistakes can hinder the simplification process:
-
Incorrect Prime Factorization: Failing to correctly identify the prime factors of a number will lead to an incorrect simplification. Always double-check your prime factorization to ensure accuracy.
-
Misunderstanding Square Root Properties: Incorrectly applying the properties of square roots, such as assuming √(a + b) = √a + √b (which is incorrect), can lead to errors. Remember that √(ab) = √a√b and √(a/b) = √a/√b are valid properties.
-
Not Simplifying Completely: Failing to simplify the expression to its most basic form is a common oversight. Always check if any perfect squares remain within the radical.
Advanced Examples of Square Root Simplification
Let's explore more complex examples to reinforce our understanding:
Example 1: Simplify √72
-
Prime Factorization: 72 = 2 x 36 = 2 x 6 x 6 = 2 x 2 x 2 x 3 x 3 = 2³ x 3²
-
Rewrite: √72 = √(2³ x 3²) = √(2² x 2 x 3²)
-
Separate: √(2² x 2 x 3²) = √2² x √3² x √2
-
Simplify: 2 x 3 x √2 = 6√2
Therefore, √72 simplifies to 6√2.
Example 2: Simplify √(48/27)
-
Simplify the fraction: 48/27 = 16/9
-
Rewrite: √(16/9) = √16 / √9
-
Simplify: 4/3
Therefore, √(48/27) simplifies to 4/3.
Example 3: Simplify √(50x²y³z⁴)
-
Prime Factorization: 50 = 2 x 5²
-
Rewrite: √(2 x 5² x x² x y² x y x z⁴)
-
Separate and Simplify: √5² x √x² x √y² x √z⁴ x √(2y) = 5xy²z²√(2y)
Therefore, √(50x²y³z⁴) simplifies to 5xy²z²√(2y).
Practical Applications and Further Exploration
The simplification of square roots is a fundamental skill applicable in numerous real-world scenarios. From calculating the length of a diagonal in a rectangular room to determining the dimensions of a geometric shape, mastering this technique provides a strong foundation for further mathematical exploration.
Understanding the concept of perfect squares and their relationship to prime factorization is crucial. This forms the basis for simplifying more complex expressions involving variables, fractions, and combinations of numbers and variables.
Further exploration could involve tackling more complex radicals, working with irrational numbers, and exploring the use of square roots in solving equations and inequalities. The knowledge gained from simplifying √12 provides a stepping stone to advanced mathematical concepts and problem-solving. Consistent practice and exploration of diverse examples are vital for strengthening your understanding and building confidence in tackling these types of problems.
Latest Posts
Latest Posts
-
An Npn Transistor Is Made Up Of
Apr 03, 2025
-
How Tall Is 48 Inches In Ft
Apr 03, 2025
-
What Is A Strait In Geography
Apr 03, 2025
-
Which Of The Following Is A Multiple Of 2
Apr 03, 2025
-
Examples Of Elements In Everyday Life
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Simplify The Square Root Of 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
