Lowest Common Denominator Of 7 And 9
Juapaving
Mar 26, 2025 · 5 min read
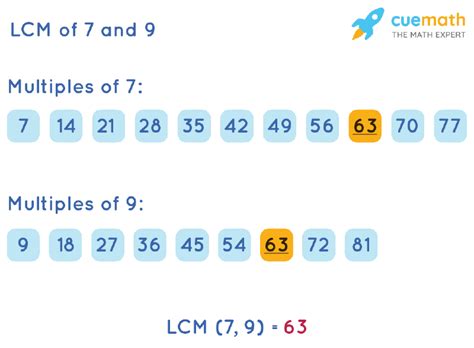
Table of Contents
Finding the Lowest Common Denominator (LCD) of 7 and 9: A Comprehensive Guide
The concept of the Lowest Common Denominator (LCD), also known as the Least Common Multiple (LCM), is a fundamental element in arithmetic and algebra. Understanding how to find the LCD is crucial for adding and subtracting fractions, simplifying expressions, and solving various mathematical problems. This comprehensive guide will delve into the process of finding the LCD of 7 and 9, exploring different methods and providing a detailed explanation of the underlying principles. We’ll also look at the broader context of LCDs and their applications.
Understanding Lowest Common Denominator (LCD) and Least Common Multiple (LCM)
Before we dive into calculating the LCD of 7 and 9, let's clarify the terminology. The Lowest Common Denominator (LCD) is the smallest number that is a multiple of two or more denominators. This term is predominantly used in the context of fractions. The Least Common Multiple (LCM), on the other hand, is the smallest positive number that is a multiple of two or more given numbers. While seemingly different, the LCD and LCM are essentially the same concept; the LCD is just the LCM applied to the denominators of fractions.
In essence, finding the LCD of 7 and 9 is equivalent to finding the LCM of 7 and 9. Since 7 and 9 are both denominators in their own right (e.g., 1/7 and 1/9), the terms are interchangeable in this specific case.
Methods for Finding the LCD of 7 and 9
There are several effective methods for determining the LCD of 7 and 9. Let's explore the most common approaches:
1. Listing Multiples Method
This is a straightforward method, particularly useful for smaller numbers like 7 and 9. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70...
- Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72...
By comparing the lists, we can see that the smallest number appearing in both lists is 63. Therefore, the LCD of 7 and 9 is 63.
2. Prime Factorization Method
This method is more efficient for larger numbers and provides a deeper understanding of the underlying mathematical principles. It involves breaking down each number into its prime factors.
- Prime factorization of 7: 7 (7 is a prime number)
- Prime factorization of 9: 3 x 3 = 3²
To find the LCM (and hence the LCD), we take the highest power of each prime factor present in the factorizations:
- The prime factors are 3 and 7.
- The highest power of 3 is 3².
- The highest power of 7 is 7.
Therefore, the LCM (and LCD) is 3² x 7 = 9 x 7 = 63.
3. Greatest Common Divisor (GCD) Method
This method utilizes the relationship between the LCM and the Greatest Common Divisor (GCD) of two numbers. The formula connecting LCM and GCD is:
LCM(a, b) x GCD(a, b) = a x b
where 'a' and 'b' are the two numbers.
First, we find the GCD of 7 and 9 using the Euclidean algorithm or other methods. Since 7 and 9 have no common factors other than 1, their GCD is 1.
Now, we can use the formula:
LCM(7, 9) x GCD(7, 9) = 7 x 9 LCM(7, 9) x 1 = 63 LCM(7, 9) = 63
Therefore, the LCD of 7 and 9 is 63.
Applications of Finding the LCD
Understanding and applying the LCD is essential in numerous mathematical contexts:
-
Adding and Subtracting Fractions: Before adding or subtracting fractions, we need to ensure they have a common denominator. The LCD makes this process simpler and more efficient. For instance, to add 1/7 and 1/9, we would convert both fractions to have the denominator of 63: (9/63) + (7/63) = 16/63
-
Simplifying Algebraic Expressions: The LCD is crucial in simplifying complex algebraic expressions involving fractions. Finding the LCD allows for combining terms and simplifying the overall expression.
-
Solving Equations: Many equations, especially those involving rational expressions (fractions with variables), require finding the LCD to solve for the unknown variable.
-
Real-world Applications: The concept of LCD finds practical application in various real-world scenarios, including:
- Measurement Conversions: Converting between different units often requires finding common denominators.
- Scheduling and Timing: Determining when events coincide (e.g., the next time two buses arrive at the same stop simultaneously) often involves calculating the LCM.
- Gear Ratios: In mechanics and engineering, the concept of LCM is used to calculate gear ratios and other mechanical relationships.
Why is the LCD Important?
The LCD is a fundamental concept because it provides a standardized way to work with fractions. Without a common denominator, adding, subtracting, and comparing fractions becomes extremely cumbersome. The LCD simplifies these operations, making them manageable and accurate. Furthermore, the ability to find the LCD is a prerequisite for tackling more advanced mathematical concepts and solving complex problems in various fields.
Beyond the Basics: Expanding on LCM and GCD
The concepts of LCM and GCD extend beyond finding the LCD of simple numbers. They are applicable to:
- More than two numbers: The methods described earlier can be extended to find the LCM or GCD of more than two numbers.
- Algebraic expressions: LCM and GCD can also be applied to algebraic expressions involving variables, allowing for simplification and manipulation of algebraic fractions.
Conclusion: Mastering the LCD of 7 and 9 and Beyond
Mastering the ability to find the lowest common denominator, whether it's for simple numbers like 7 and 9 or more complex scenarios, is a cornerstone of mathematical proficiency. This guide has explored various methods for calculating the LCD of 7 and 9, demonstrating that the answer is 63. More importantly, it highlighted the broader significance of the LCD in simplifying fractions, solving equations, and tackling a wide range of mathematical problems, extending to real-world applications. A strong grasp of this fundamental concept will pave the way for success in higher-level mathematics and related fields. Remember to practice using different methods to solidify your understanding and build confidence in tackling more complex problems.
Latest Posts
Latest Posts
-
List All The Factors Of 15
Mar 29, 2025
-
Is The Square Root Of 72 Rational Or Irrational
Mar 29, 2025
-
One Pair Of Opposite Sides Are Parallel
Mar 29, 2025
-
What Is The Relationship Between Density Mass And Volume
Mar 29, 2025
-
Difference Between Seed Germination And Seed Emergence
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about Lowest Common Denominator Of 7 And 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
