One Pair Of Opposite Sides Are Parallel
Juapaving
Mar 29, 2025 · 6 min read
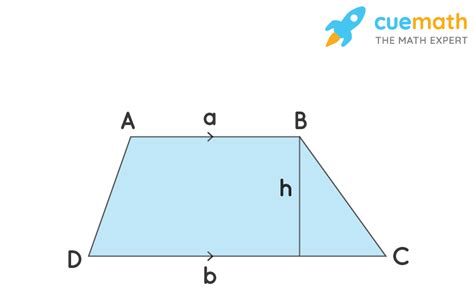
Table of Contents
One Pair of Opposite Sides are Parallel: Exploring the Properties of Trapezoids
Understanding geometric shapes is fundamental to various fields, from architecture and engineering to computer graphics and data visualization. Among the diverse array of quadrilaterals—four-sided polygons—trapezoids hold a unique position, defined by the crucial property: one pair of opposite sides are parallel. This seemingly simple characteristic unlocks a wealth of interesting properties and theorems, which we will explore in detail in this comprehensive guide.
Defining the Trapezoid: More Than Just Parallel Sides
A trapezoid, also known as a trapezium in some regions, is a quadrilateral with at least one pair of parallel sides. This defining characteristic sets it apart from other quadrilaterals like parallelograms, rectangles, and squares, which have two pairs of parallel sides. The parallel sides are called bases, often denoted as b1 and b2. The non-parallel sides are called legs.
It's crucial to understand that the definition only mandates at least one pair of parallel sides. This implies that while some trapezoids might exhibit additional properties—like isosceles trapezoids, which possess congruent legs—the fundamental defining property remains the parallelism of one pair of opposite sides.
Types of Trapezoids: A Closer Look at Variations
While the basic definition encompasses a broad range of shapes, classifying trapezoids into specific types helps us understand their unique geometric characteristics.
1. Isosceles Trapezoid: Symmetry and Congruence
An isosceles trapezoid is a trapezoid where the non-parallel sides (legs) are congruent. This symmetry leads to several noteworthy properties:
- Base angles are congruent: The angles adjacent to each base are equal in measure. This means that ∠A = ∠B and ∠C = ∠D in an isosceles trapezoid ABCD, where AB || CD.
- Diagonals are congruent: The lengths of the diagonals AC and BD are equal.
- Reflectional Symmetry: An isosceles trapezoid exhibits reflectional symmetry about a line perpendicular to the bases and passing through the midpoints of both bases.
2. Right Trapezoid: A Right Angle Connection
A right trapezoid is a trapezoid with at least one right angle. This means one of the legs is perpendicular to both bases. This simple addition dramatically simplifies calculations involving area and other geometric properties. It's particularly useful in practical applications where right angles are commonly encountered in construction and engineering.
3. Scalene Trapezoid: The General Case
A scalene trapezoid is simply a trapezoid that does not fit the descriptions of an isosceles or right trapezoid. It has no special symmetries or congruent sides or angles beyond the basic parallel sides definition. It represents the most general case of trapezoids and serves as a good reminder that the parallel sides are the defining feature, rather than any specific angles or side lengths.
Key Properties and Theorems of Trapezoids
Understanding the properties and theorems related to trapezoids is crucial for solving various geometric problems. Let's delve into some key concepts:
1. Midsegment Theorem: Connecting the Midpoints
The midsegment theorem states that the segment connecting the midpoints of the legs of a trapezoid is parallel to the bases and its length is half the sum of the lengths of the bases. This theorem proves incredibly useful in determining unknown lengths within a trapezoid. The midsegment, often denoted as m, can be calculated as:
m = ( b1 + b2 ) / 2
where b1 and b2 are the lengths of the bases.
2. Area Calculation: Finding the Enclosed Space
Calculating the area of a trapezoid relies on the lengths of its bases and its height. The height is the perpendicular distance between the parallel bases. The formula for the area (A) of a trapezoid is:
A = (1/2) * h * (b1 + b2)
where h is the height, and b1 and b2 are the lengths of the bases. This formula highlights the importance of understanding both the parallel sides and the perpendicular distance between them.
3. Angle Relationships: Exploring Supplementary and Congruent Angles
In a trapezoid, the sum of adjacent angles along a leg is always 180 degrees (supplementary angles). This is a direct consequence of the parallel lines forming transversal lines with the legs. Furthermore, in an isosceles trapezoid, base angles are congruent. These angle relationships are frequently utilized in proving other geometric theorems or in solving problems involving unknown angles.
Practical Applications and Real-World Examples
Trapezoids are surprisingly common in the real world, often appearing in architecture, design, and engineering:
- Architecture: The roofs of many buildings, particularly those with sloping sides, are shaped like trapezoids.
- Civil Engineering: Trapezoidal channels are frequently used for irrigation and drainage systems due to their efficient water flow properties.
- Graphic Design and Computer Graphics: Trapezoidal shapes are used extensively in creating visuals and illustrations, adding dynamism and visual interest.
- Mechanical Engineering: Components and parts in many machines incorporate trapezoidal shapes to optimize functionality and design.
Understanding the properties of trapezoids allows us to accurately model and analyze these real-world structures and systems.
Solving Problems Involving Trapezoids: A Step-by-Step Guide
Let's illustrate the application of trapezoid properties through a few example problems:
Problem 1: Finding the Midsegment
A trapezoid has bases of length 8 cm and 12 cm. What is the length of the midsegment?
Solution:
Using the midsegment theorem, we have:
m = ( b1 + b2 ) / 2 = (8 cm + 12 cm) / 2 = 10 cm
Problem 2: Calculating the Area
A trapezoid has bases of 6 inches and 10 inches, and a height of 4 inches. What is its area?
Solution:
Using the area formula, we get:
A = (1/2) * h * (b1 + b2) = (1/2) * 4 inches * (6 inches + 10 inches) = 32 square inches
Problem 3: Determining Unknown Angles
In an isosceles trapezoid, one base angle measures 70 degrees. What are the measures of the other angles?
Solution:
Since base angles are congruent in an isosceles trapezoid, the other base angle also measures 70 degrees. The adjacent angles to a leg are supplementary, so the other two angles will be 180 - 70 = 110 degrees each.
Beyond the Basics: Advanced Concepts and Further Exploration
While this guide covers the fundamental aspects of trapezoids, deeper exploration can reveal further complexities and connections to other areas of mathematics. Topics for further study include:
- Coordinate Geometry and Trapezoids: Representing trapezoids using coordinate systems and applying vector methods for solving problems.
- Calculus and Trapezoids: Using trapezoidal approximations for integration and calculating areas under curves.
- Advanced Geometric Theorems: Exploring more complex theorems related to circumscribed and inscribed circles within trapezoids and the relationships between their various elements.
By delving deeper into these advanced concepts, one can gain a much more comprehensive and sophisticated understanding of trapezoids and their place within the broader landscape of geometry.
Conclusion: The Enduring Importance of Trapezoids
Trapezoids, defined by the simple yet powerful property of having one pair of parallel sides, reveal a rich tapestry of geometric properties and theorems. Their presence in various real-world applications, from architecture to engineering, underscores their practical importance. Understanding the nuances of trapezoids—their different types, properties, and related theorems—is not merely an academic exercise, but a valuable skill with practical relevance across numerous disciplines. Whether you are a student of geometry, a budding engineer, or simply someone fascinated by the elegance of mathematical shapes, the humble trapezoid deserves a closer look and a deeper appreciation.
Latest Posts
Latest Posts
-
What Is The Lcm Of 2 3 And 6
Mar 31, 2025
-
What Ratio Is The Same As 2 3
Mar 31, 2025
-
The Role Of Hydrochloric Acid In Protein Digestion Is To
Mar 31, 2025
-
Is Dna Copied Before Meiosis 2
Mar 31, 2025
-
How Were The Mauryan And Gupta Empires Alike
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about One Pair Of Opposite Sides Are Parallel . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
