Is The Square Root Of 72 Rational Or Irrational
Juapaving
Mar 29, 2025 · 5 min read
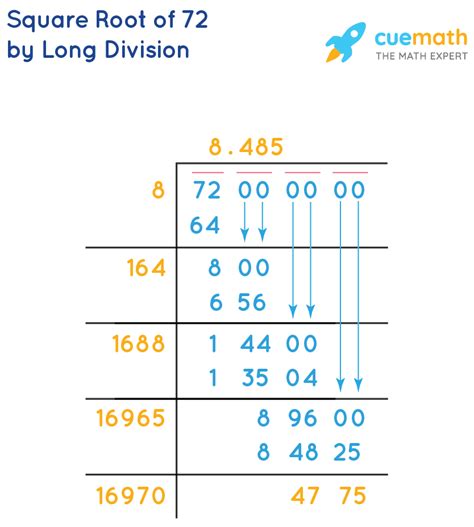
Table of Contents
Is the Square Root of 72 Rational or Irrational? A Deep Dive into Number Theory
The question of whether the square root of 72 is rational or irrational might seem simple at first glance. However, delving into this seemingly basic problem opens a door to a fascinating exploration of number theory, revealing the fundamental distinctions between rational and irrational numbers and highlighting the elegance of mathematical proofs. This article will not only answer the question definitively but also provide a comprehensive understanding of the underlying concepts, equipping you with the tools to tackle similar problems.
Understanding Rational and Irrational Numbers
Before we tackle the square root of 72, let's solidify our understanding of the core concepts: rational and irrational numbers.
Rational Numbers: These are numbers that can be expressed as a fraction p/q, where p and q are integers, and q is not zero. Examples include 1/2, 3/4, -5/7, and even whole numbers like 5 (which can be expressed as 5/1). The key characteristic is the ability to represent the number precisely as a ratio of two integers.
Irrational Numbers: These numbers cannot be expressed as a fraction of two integers. Their decimal representations are non-terminating (they don't end) and non-repeating (they don't have a recurring pattern). Famous examples include π (pi), e (Euler's number), and the square root of most non-perfect squares.
Analyzing the Square Root of 72
Now, let's focus on √72. To determine if it's rational or irrational, we need to investigate whether it can be simplified into a fraction of two integers.
First, let's simplify √72 by finding its prime factorization.
72 = 2 x 36 = 2 x 2 x 18 = 2 x 2 x 2 x 9 = 2 x 2 x 2 x 3 x 3 = 2³ x 3²
Therefore, √72 = √(2³ x 3²) = √(2² x 2 x 3²) = √2² x √2 x √3² = 2 x 3 x √2 = 6√2
This simplification reveals a crucial point: the square root of 72 is equivalent to 6 multiplied by the square root of 2. We know that the square root of 2 is a classic example of an irrational number. It's decimal representation is non-terminating and non-repeating (approximately 1.41421356...).
Since √2 is irrational, and multiplying an irrational number by a rational number (6 in this case) always results in an irrational number, we can conclude:
The square root of 72 is irrational.
Proof by Contradiction: A Formal Approach
We can further solidify this conclusion using a powerful mathematical technique called proof by contradiction. This method assumes the opposite of what we want to prove and then demonstrates that this assumption leads to a contradiction, thereby proving the original statement.
Let's assume, for the sake of contradiction, that √72 is rational. This means it can be expressed as a fraction p/q, where p and q are integers, q ≠ 0, and p and q are in their simplest form (meaning they have no common factors other than 1).
If √72 = p/q, then squaring both sides gives:
72 = p²/q²
Rearranging, we get:
72q² = p²
This equation tells us that p² is an even number (because it's a multiple of 72). If p² is even, then p must also be even (because the square of an odd number is always odd). Therefore, we can express p as 2k, where k is an integer.
Substituting p = 2k into the equation above:
72q² = (2k)² = 4k²
Dividing both sides by 4:
18q² = k²
This equation now shows that k² is also an even number, which means k must be even as well.
We've arrived at a contradiction. We initially assumed that p and q had no common factors. However, we've shown that both p and q must be even, meaning they share a common factor of 2. This contradicts our initial assumption. Therefore, our initial assumption that √72 is rational must be false.
Consequently, √72 is irrational.
Expanding the Understanding: Irrationality of Square Roots
The irrationality of √72 is a specific instance of a broader principle: the square root of any non-perfect square integer is irrational. A perfect square is a number that can be obtained by squaring an integer (e.g., 1, 4, 9, 16, etc.). If a number is not a perfect square, its square root will always be irrational. This can be proven using similar methods to the proof by contradiction demonstrated above.
Practical Implications and Further Exploration
Understanding the distinction between rational and irrational numbers is crucial in various fields, including:
- Computer Science: Representing irrational numbers in computer systems often requires approximations, leading to potential errors in calculations.
- Engineering: Precision in engineering calculations often demands a clear understanding of the limitations associated with approximating irrational numbers.
- Physics: Many physical constants, such as the speed of light and gravitational constant, are irrational numbers.
This exploration into the square root of 72 serves as a stepping stone for deeper investigations into number theory. You can further your understanding by exploring topics such as:
- Transcendental numbers: A subset of irrational numbers that cannot be the root of any polynomial equation with rational coefficients (e.g., π and e).
- Continued fractions: An alternative way to represent irrational numbers that can provide increasingly accurate approximations.
- Approximating irrational numbers: Exploring different methods for finding rational approximations of irrational numbers with varying levels of accuracy.
Conclusion
The seemingly simple question of whether the square root of 72 is rational or irrational has led us on a journey into the heart of number theory. We've established definitively that √72 is irrational, both through simplification and rigorous proof by contradiction. This exploration has provided a solid foundation for understanding the fundamental difference between rational and irrational numbers and highlights the beauty and power of mathematical reasoning. The implications of this understanding extend far beyond the realm of pure mathematics, impacting various scientific and computational fields. By grasping these core concepts, you're equipped to approach more complex mathematical problems with confidence and a deeper appreciation for the intricate world of numbers.
Latest Posts
Latest Posts
-
What Are More Things About The Major Components Of Soil
Apr 01, 2025
-
What Is The Lcm Of 5 6 7
Apr 01, 2025
-
Find The Complementary And Supplementary Angles
Apr 01, 2025
-
What Is The Specific Heat Of Liquid Water
Apr 01, 2025
-
Round 415 To The Nearest Hundred
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Is The Square Root Of 72 Rational Or Irrational . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
