Least Common Multiple Of 6 7 9
Juapaving
Mar 24, 2025 · 5 min read
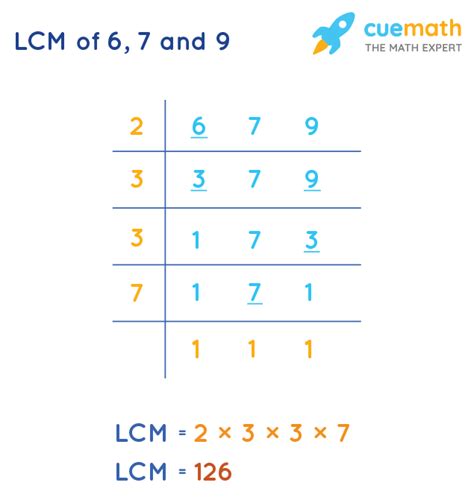
Table of Contents
Finding the Least Common Multiple (LCM) of 6, 7, and 9: A Comprehensive Guide
The least common multiple (LCM) is a fundamental concept in number theory and arithmetic. It represents the smallest positive integer that is a multiple of all the integers in a given set. This article will delve deep into calculating the LCM of 6, 7, and 9, exploring various methods and illustrating their applications. We'll move beyond a simple answer, providing a robust understanding of the underlying principles and demonstrating how to solve similar problems effectively.
Understanding the Least Common Multiple (LCM)
Before diving into the specifics of finding the LCM of 6, 7, and 9, let's solidify our understanding of the LCM itself. The LCM is the smallest positive integer that is divisible by all the numbers in a given set without leaving a remainder. This concept is crucial in various mathematical applications, from simplifying fractions to solving problems involving cyclical events.
Consider two numbers, a and b. Their LCM, denoted as LCM(a, b), is the smallest positive integer that is a multiple of both a and b. This extends to sets of more than two numbers. For example, the LCM of 6, 7, and 9 is the smallest positive integer that is divisible by 6, 7, and 9.
Methods for Calculating the LCM
Several methods exist for calculating the LCM, each with its own strengths and weaknesses. We will explore the most common approaches, illustrating each with the example of finding the LCM of 6, 7, and 9.
1. Listing Multiples Method
This method involves listing the multiples of each number until a common multiple is found. While straightforward for smaller numbers, it becomes less efficient as the numbers get larger.
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 63, 72, 78, 84, 90, 96, 102, 108, 114, 120, 126...
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91, 98, 105, 112, 119, 126...
- Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99, 108, 117, 126...
By examining the lists, we can see that the smallest common multiple is 126. Therefore, LCM(6, 7, 9) = 126. This method is simple to understand but can be time-consuming for larger numbers.
2. Prime Factorization Method
This method is generally more efficient, especially for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor present.
- Prime factorization of 6: 2 × 3
- Prime factorization of 7: 7 (7 is a prime number)
- Prime factorization of 9: 3 × 3 = 3²
To find the LCM, we take the highest power of each prime factor present in the factorizations: 2¹, 3², and 7¹. Multiplying these together gives us: 2 × 3 × 3 × 7 = 126. Therefore, LCM(6, 7, 9) = 126.
3. Greatest Common Divisor (GCD) Method
This method utilizes the relationship between the LCM and the greatest common divisor (GCD) of two numbers. The formula relating the LCM and GCD is:
LCM(a, b) = (a × b) / GCD(a, b)
This formula can be extended to multiple numbers, but it requires calculating the GCD iteratively. Let's illustrate this with our example:
- GCD(6, 7): Since 6 and 7 have no common factors other than 1, GCD(6, 7) = 1.
- LCM(6, 7): LCM(6, 7) = (6 × 7) / 1 = 42
- GCD(42, 9): The common factors of 42 and 9 are only 3. Therefore, GCD(42, 9) = 3.
- LCM(42, 9): LCM(42, 9) = (42 × 9) / 3 = 126
Therefore, LCM(6, 7, 9) = 126. This method is efficient for larger numbers if you have an efficient method for calculating the GCD, such as the Euclidean algorithm.
Applications of LCM
The LCM has a wide range of applications in various fields, including:
-
Fractions: Finding the LCM of the denominators is essential when adding or subtracting fractions. This allows us to find a common denominator, simplifying the calculation.
-
Scheduling: The LCM is used to determine when events with different periodicities will occur simultaneously. For example, if one event occurs every 6 days, another every 7 days, and a third every 9 days, the LCM(6, 7, 9) = 126 will tell us that all three events will occur together again on the 126th day.
-
Modular Arithmetic: The LCM plays a critical role in solving problems related to congruences and modular arithmetic, a branch of number theory with applications in cryptography and computer science.
-
Music Theory: The LCM is used in music theory to find the least common multiple of the note durations in different musical parts, which is important for synchronization and timing.
Extending the Concept: LCM of Larger Sets of Numbers
The methods described above can be extended to find the LCM of larger sets of numbers. The prime factorization method remains a particularly powerful approach for this. For example, to find the LCM of 6, 7, 9, and 10:
-
Prime factorization:
- 6 = 2 × 3
- 7 = 7
- 9 = 3²
- 10 = 2 × 5
-
Identify the highest power of each prime factor: 2¹, 3², 5¹, 7¹
-
Calculate the LCM: 2 × 3 × 3 × 5 × 7 = 630. Therefore, LCM(6, 7, 9, 10) = 630.
Conclusion: Mastering LCM Calculations
Understanding and mastering the calculation of the least common multiple is a valuable skill with wide-ranging applications in mathematics and beyond. This article has explored various methods for calculating the LCM, demonstrating their effectiveness through the example of finding the LCM of 6, 7, and 9. Whether you use the listing multiples method, the prime factorization method, or the GCD method, the key is to choose the approach that best suits the numbers involved and your comfort level. By understanding the underlying principles and practicing these methods, you will build a strong foundation in number theory and enhance your problem-solving capabilities. Remember that the prime factorization method generally provides the most efficient approach, especially for larger sets of numbers. This method’s elegance and efficiency make it a preferred technique for both manual calculations and algorithmic implementations. Practice applying these techniques and explore the various applications of LCM to solidify your understanding and broaden your mathematical skillset.
Latest Posts
Latest Posts
-
What Is The Lcm Of 5 And 7
Mar 29, 2025
-
Least Common Multiple Of 6 9 And 15
Mar 29, 2025
-
Words Beginning And Ending In T
Mar 29, 2025
-
Light Microscope Vs Transmission Electron Microscope
Mar 29, 2025
-
What Is The Square Root Of 37
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about Least Common Multiple Of 6 7 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
