What Is The Square Root Of 37
Juapaving
Mar 29, 2025 · 5 min read
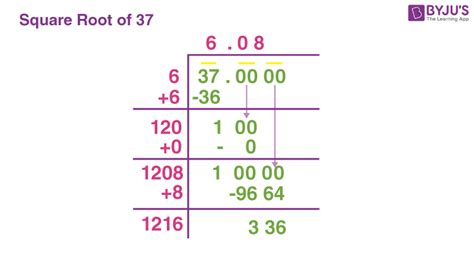
Table of Contents
What is the Square Root of 37? A Deep Dive into Irrational Numbers
The seemingly simple question, "What is the square root of 37?" opens a fascinating window into the world of mathematics, specifically the realm of irrational numbers. While a simple calculator might offer a decimal approximation, understanding the true nature of √37 requires exploring concepts beyond just numerical answers. This article delves deep into the meaning of square roots, the properties of irrational numbers, and various methods for approximating √37, catering to both beginners and those seeking a more advanced understanding.
Understanding Square Roots
The square root of a number is a value that, when multiplied by itself, equals the original number. In simpler terms, it's the inverse operation of squaring a number. For example:
- The square root of 9 (√9) is 3, because 3 x 3 = 9.
- The square root of 16 (√16) is 4, because 4 x 4 = 16.
However, not all numbers have perfect square roots – integers that result in whole numbers. This is where the concept of irrational numbers comes into play.
Irrational Numbers: The Nature of √37
The square root of 37 (√37) is an irrational number. This means it cannot be expressed as a simple fraction (a ratio of two integers). Its decimal representation is non-terminating and non-repeating; it goes on forever without any pattern. This is a fundamental characteristic of many square roots of non-perfect squares.
Unlike rational numbers like 1/2 (0.5) or 3/4 (0.75), irrational numbers cannot be precisely represented as a finite decimal. This is why calculators provide only approximations of √37.
Approximating √37: Different Methods
Since we can't express √37 exactly as a fraction or a finite decimal, we rely on approximation methods. Several techniques exist, each with varying levels of accuracy and complexity:
1. Using a Calculator: The Quickest Method
The most straightforward method is to use a calculator. Most scientific calculators have a square root function (√). Simply input 37 and press the square root button. The calculator will provide a decimal approximation, typically accurate to several decimal places. This is usually sufficient for most practical applications. For instance, a calculator might give you:
√37 ≈ 6.08276253
However, remember this is an approximation. The actual value continues infinitely beyond the displayed digits.
2. The Babylonian Method (or Heron's Method): An Iterative Approach
This ancient method is an iterative algorithm that refines an initial guess to obtain a progressively more accurate approximation. It works by repeatedly averaging the current guess with the number divided by the guess.
Here's how it works for √37:
-
Start with an initial guess: Let's guess 6, as 6 x 6 = 36, which is close to 37.
-
Iterate:
- Divide 37 by the guess: 37 / 6 ≈ 6.1667
- Average the guess and the result: (6 + 6.1667) / 2 ≈ 6.0833
-
Repeat: Use the result (6.0833) as the new guess and repeat step 2. The more iterations you perform, the closer the approximation gets to the true value of √37.
After several iterations, you'll obtain a highly accurate approximation. The Babylonian method demonstrates a powerful iterative approach to solving problems that don't have a direct, closed-form solution.
3. Using the Taylor Series Expansion: A More Advanced Approach
For those familiar with calculus, the Taylor series expansion provides a method to approximate the square root of a number. This involves representing the square root function as an infinite sum of terms. While conceptually more complex, it offers a high degree of accuracy with enough terms. This method is beyond the scope of a basic explanation but is worth mentioning for its mathematical elegance.
4. Linear Approximation: A Simple Graphical Method
A simple graphical approach involves using a tangent line to the function y = √x at a nearby point with a known square root. For instance, using the point (36, 6), you can calculate the slope of the tangent line and use it to estimate the value of √37. This method provides a less precise approximation compared to the Babylonian method or calculator but offers a visual understanding of the concept.
Practical Applications of √37
While seemingly abstract, understanding and approximating irrational numbers like √37 has various practical applications across numerous fields:
-
Engineering and Physics: Calculations involving distances, areas, and volumes often necessitate square roots. For example, determining the length of the diagonal of a rectangle or calculating the speed of an object using the Pythagorean theorem might involve irrational square roots.
-
Computer Graphics and Game Development: Rendering 3D environments and simulating physics in video games requires extensive use of square root calculations for distance calculations, vector normalization, and collision detection.
-
Financial Modeling: Mathematical models used in finance and economics often employ square roots in calculations related to standard deviation, risk assessment, and portfolio optimization.
-
Statistics: The standard deviation, a crucial measure of data dispersion, frequently involves calculating the square root of a variance.
Conclusion: Beyond the Decimal Approximation
The square root of 37 is more than just a number displayed on a calculator screen. It represents a fundamental concept in mathematics, highlighting the beauty and complexity of irrational numbers. Understanding its nature, the various approximation techniques, and its real-world applications enriches our appreciation of the mathematical world around us. Whether you use a calculator for a quick approximation or delve into more sophisticated methods, understanding the concept of √37 offers valuable insights into the fundamental building blocks of mathematics and its wide-ranging impact on various fields. The pursuit of understanding irrational numbers, like √37, continues to be a significant area of mathematical exploration and application.
Latest Posts
Latest Posts
-
An Objects Resistance To A Change In Motion
Mar 31, 2025
-
Why Is The Earth Called A Unique Planet Short Answer
Mar 31, 2025
-
Eukaryotic Cells Are Much More Complex Than Prokaryotic Cells Because
Mar 31, 2025
-
Prokaryotic And Eukaryotic Cells Answer Key
Mar 31, 2025
-
Words That Begin With A A
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Is The Square Root Of 37 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
