Least Common Multiple Of 6 9 And 15
Juapaving
Mar 29, 2025 · 5 min read
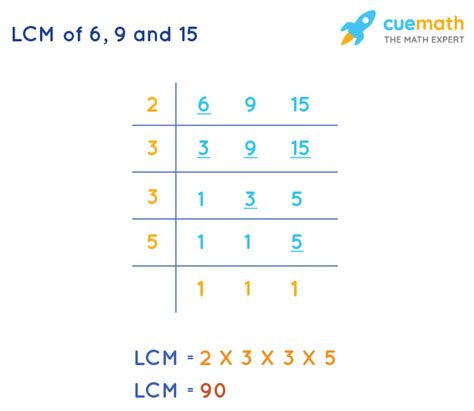
Table of Contents
Finding the Least Common Multiple (LCM) of 6, 9, and 15: A Comprehensive Guide
The least common multiple (LCM) is a fundamental concept in mathematics, particularly in number theory and arithmetic. It represents the smallest positive integer that is a multiple of all the integers in a given set. Understanding how to find the LCM is crucial for various applications, from simplifying fractions to solving problems in algebra and beyond. This article delves into the process of calculating the LCM of 6, 9, and 15, exploring various methods and providing a comprehensive understanding of the underlying principles.
Understanding Least Common Multiples
Before diving into the calculation, let's solidify our understanding of LCM. The LCM of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. For instance, the LCM of 2 and 3 is 6 because 6 is the smallest positive integer divisible by both 2 and 3.
Key Characteristics of LCM:
- Positive Integer: The LCM is always a positive integer.
- Smallest Multiple: It's the smallest number that's a multiple of all the given integers.
- Divisibility: All the given integers divide the LCM without leaving a remainder.
Methods for Finding the LCM of 6, 9, and 15
There are several effective methods to determine the LCM of a set of integers. We'll explore three common approaches: the listing method, the prime factorization method, and the greatest common divisor (GCD) method.
1. The Listing Method
The listing method, while straightforward, can become cumbersome for larger numbers. It involves listing the multiples of each number until a common multiple is found.
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 78, 84, 90...
- Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72, 81, 90...
- Multiples of 15: 15, 30, 45, 60, 75, 90...
By comparing the lists, we observe that the smallest common multiple of 6, 9, and 15 is 90. This method works well for smaller numbers but becomes less efficient as the numbers increase in size.
2. The Prime Factorization Method
The prime factorization method is a more efficient and systematic approach, particularly for larger numbers. It involves expressing each number as a product of its prime factors.
- Prime Factorization of 6: 2 x 3
- Prime Factorization of 9: 3 x 3 = 3²
- Prime Factorization of 15: 3 x 5
To find the LCM, we select the highest power of each prime factor present in the factorizations:
- The highest power of 2 is 2¹ = 2
- The highest power of 3 is 3² = 9
- The highest power of 5 is 5¹ = 5
Multiplying these highest powers together, we get: 2 x 3² x 5 = 2 x 9 x 5 = 90. Therefore, the LCM of 6, 9, and 15 is 90. This method is generally preferred for its efficiency and applicability to larger numbers.
3. The Greatest Common Divisor (GCD) Method
The GCD method utilizes the relationship between the LCM and the GCD (greatest common divisor) of two or more numbers. The formula connecting LCM and GCD is:
LCM(a, b) * GCD(a, b) = a * b
While this formula is initially defined for two numbers, it can be extended to multiple numbers through iterative application. First, we find the GCD of 6 and 9 using the Euclidean algorithm or prime factorization.
- Prime Factorization of 6: 2 x 3
- Prime Factorization of 9: 3 x 3 = 3²
The GCD(6, 9) is 3. Now, we find the LCM(6, 9) using the formula:
LCM(6, 9) * GCD(6, 9) = 6 * 9 LCM(6, 9) * 3 = 54 LCM(6, 9) = 18
Next, we find the LCM of 18 and 15 using the same approach.
- Prime Factorization of 18: 2 x 3²
- Prime Factorization of 15: 3 x 5
GCD(18, 15) = 3
LCM(18, 15) * GCD(18, 15) = 18 * 15 LCM(18, 15) * 3 = 270 LCM(18, 15) = 90
Therefore, the LCM of 6, 9, and 15 is 90. This method demonstrates the interconnectedness between LCM and GCD and provides an alternative pathway to the solution.
Applications of LCM
The concept of LCM finds practical applications in various fields:
- Fraction Addition and Subtraction: Finding a common denominator for adding or subtracting fractions involves determining the LCM of the denominators.
- Scheduling and Planning: LCM is useful in scheduling events that occur at regular intervals, such as determining when two cyclical processes will coincide. For example, if event A happens every 6 days and event B happens every 9 days, the LCM helps find when both events will happen on the same day.
- Music Theory: LCM plays a role in understanding musical intervals and harmonies.
- Gear Ratios: In mechanical engineering, LCM is used in calculations involving gear ratios and synchronization of rotating components.
Beyond the Basics: LCM and Advanced Concepts
The understanding of LCM extends beyond simple calculations. It forms a foundation for more advanced mathematical concepts:
- Modular Arithmetic: LCM is essential in modular arithmetic, used in cryptography and computer science.
- Abstract Algebra: LCM generalizes to concepts in abstract algebra, particularly in ring theory and ideal theory.
Conclusion: Mastering the LCM
Finding the least common multiple is a fundamental skill in mathematics with wide-ranging applications. This article explored various methods for calculating the LCM of 6, 9, and 15, highlighting the strengths and weaknesses of each approach. The prime factorization method generally offers the most efficient and systematic solution, particularly for larger numbers. Understanding LCM is crucial for success in various mathematical and practical applications, and mastering these techniques will enhance your mathematical proficiency. Remember, practice is key to solidifying your understanding and becoming comfortable with these calculations. The more you work with LCM problems, the easier it will become to identify the most efficient method for each situation.
Latest Posts
Latest Posts
-
Molar Mass Of Al Oh 3
Mar 31, 2025
-
An Objects Resistance To A Change In Motion
Mar 31, 2025
-
Why Is The Earth Called A Unique Planet Short Answer
Mar 31, 2025
-
Eukaryotic Cells Are Much More Complex Than Prokaryotic Cells Because
Mar 31, 2025
-
Prokaryotic And Eukaryotic Cells Answer Key
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Least Common Multiple Of 6 9 And 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
