Least Common Multiple Of 14 And 4
Juapaving
Mar 28, 2025 · 5 min read
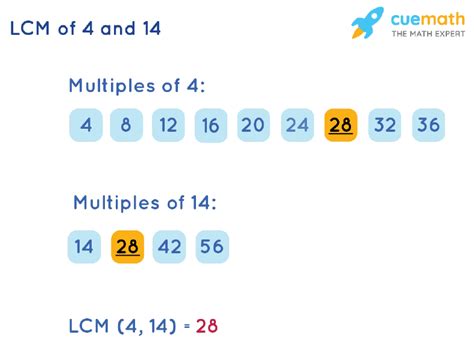
Table of Contents
Unveiling the Least Common Multiple (LCM) of 14 and 4: A Deep Dive
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts and various methods for calculating it opens doors to more advanced mathematical concepts. This article delves into the LCM of 14 and 4, exploring multiple approaches – from prime factorization to the Euclidean algorithm – and highlighting its significance in various applications. We’ll go beyond a simple answer, providing a comprehensive understanding of the LCM and its relevance.
Understanding Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. It's a fundamental concept in number theory and finds applications in various fields, including scheduling, music theory, and computer science. Think of it as the smallest number that all your chosen numbers can divide into evenly.
For instance, let's consider the numbers 2 and 3. Their multiples are:
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20...
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30...
The common multiples are 6, 12, 18, 24... The least common multiple is 6.
Calculating the LCM of 14 and 4: Method 1 – Prime Factorization
The prime factorization method is a powerful and widely used technique for determining the LCM of any set of numbers. It involves breaking down each number into its prime factors. Let's apply this to 14 and 4:
1. Prime Factorization of 14:
14 = 2 x 7
2. Prime Factorization of 4:
4 = 2 x 2 = 2²
3. Identifying Common and Unique Prime Factors:
Both 14 and 4 share a common prime factor of 2. However, 14 has a unique prime factor of 7, and 4 has an additional 2 as a prime factor.
4. Constructing the LCM:
To find the LCM, we take the highest power of each prime factor present in the factorizations and multiply them together:
LCM(14, 4) = 2² x 7 = 4 x 7 = 28
Therefore, the least common multiple of 14 and 4 is 28. This means 28 is the smallest positive integer that is divisible by both 14 and 4.
Calculating the LCM of 14 and 4: Method 2 – Listing Multiples
This method is straightforward but can become cumbersome for larger numbers. We list the multiples of each number until we find the smallest common multiple.
Multiples of 14: 14, 28, 42, 56, 70, 84, 98, 112, ...
Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, ...
The smallest number that appears in both lists is 28. Thus, the LCM(14, 4) = 28.
Calculating the LCM of 14 and 4: Method 3 – Using the Greatest Common Divisor (GCD)
The LCM and GCD (greatest common divisor) of two numbers are closely related. They are connected by the following formula:
LCM(a, b) = (|a x b|) / GCD(a, b)
Where:
- a and b are the two numbers
- |a x b| represents the absolute value of the product of a and b
- GCD(a, b) is the greatest common divisor of a and b
1. Finding the GCD of 14 and 4 using the Euclidean Algorithm:
The Euclidean algorithm is an efficient method for finding the GCD of two numbers. It involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCD.
- 14 = 3 x 4 + 2
- 4 = 2 x 2 + 0
The GCD(14, 4) = 2
2. Calculating the LCM:
LCM(14, 4) = (|14 x 4|) / GCD(14, 4) = (56) / 2 = 28
This confirms that the LCM of 14 and 4 is 28.
The Significance of LCM
The concept of LCM extends beyond simple arithmetic exercises. It has practical applications in diverse fields:
-
Scheduling: Imagine two events occurring at different intervals. The LCM helps determine when both events will coincide. For example, if one event happens every 14 days and another every 4 days, they will coincide every 28 days.
-
Music Theory: LCM plays a role in understanding musical harmony and rhythm. The LCM of two note durations determines the smallest time interval after which both durations will align perfectly.
-
Computer Science: In programming, LCM is used in tasks involving synchronization, scheduling processes, and optimizing algorithms.
-
Engineering and Construction: In construction projects, materials often need to be cut into specific lengths. The LCM can determine the largest equal pieces that can be cut from multiple lengths of material.
-
Fractions: The LCM is crucial when adding or subtracting fractions with different denominators. Finding the LCM of the denominators allows you to convert the fractions to a common denominator for simpler calculations.
Beyond the Basics: LCM of More Than Two Numbers
The methods described above can be extended to find the LCM of more than two numbers. For the prime factorization method, you'd simply find the prime factorization of each number, identify all the unique prime factors with their highest powers, and multiply them together. For the GCD method, you'd need to iteratively find the GCD of pairs of numbers and then use the relationship between LCM and GCD.
For example, to find the LCM of 14, 4, and 6:
-
Prime Factorization:
- 14 = 2 x 7
- 4 = 2²
- 6 = 2 x 3
-
Identifying Prime Factors: The unique prime factors are 2, 3, and 7. The highest powers are 2², 3¹, and 7¹.
-
Calculating LCM: LCM(14, 4, 6) = 2² x 3 x 7 = 84
Conclusion
Finding the least common multiple of 14 and 4, which is 28, is a simple calculation, but the underlying concepts and methods are essential building blocks in mathematics and various applied fields. Understanding the prime factorization method, the listing multiples method, and the relationship between LCM and GCD provides a solid foundation for tackling more complex problems involving multiples and divisors. The versatility of LCM in scheduling, music, computer science, and other areas highlights its significance as a fundamental concept in mathematics. The ability to efficiently calculate the LCM and understand its implications is a valuable asset in numerous contexts.
Latest Posts
Latest Posts
-
Do The Diagonals Of A Kite Bisect Teachother
Mar 31, 2025
-
What Is The Factor Of 71
Mar 31, 2025
-
Force Per Unit Area Is Termed
Mar 31, 2025
-
Consecutive Angles Of A Parallelogram Are Supplementary
Mar 31, 2025
-
What Are 5 Examples Of Chemical Weathering
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Least Common Multiple Of 14 And 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
