Is The Square Root Of 45 A Rational Number
Juapaving
Apr 01, 2025 · 5 min read
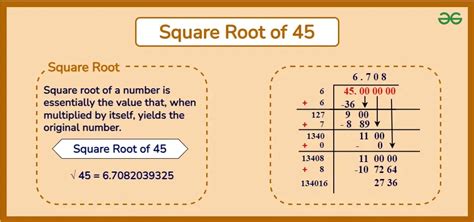
Table of Contents
Is the Square Root of 45 a Rational Number? A Deep Dive into Irrationality
The question of whether the square root of 45 is a rational number is a fundamental one in mathematics, touching upon the core concepts of rational and irrational numbers. Understanding this requires a solid grasp of these definitions and some number theory. This article will delve deep into the matter, providing a comprehensive explanation accessible to both beginners and those with a more advanced mathematical background.
Understanding Rational and Irrational Numbers
Before we tackle the square root of 45, let's define our terms:
Rational Numbers: A rational number is any number that can be expressed as a fraction p/q, where p and q are integers, and q is not equal to zero. Examples include 1/2, 3/4, -5/7, and even integers like 4 (which can be written as 4/1). The decimal representation of a rational number either terminates (e.g., 0.75) or repeats in a predictable pattern (e.g., 0.333...).
Irrational Numbers: An irrational number is any number that cannot be expressed as a fraction of two integers. Their decimal representations are non-terminating and non-repeating. Famous examples include π (pi), e (Euler's number), and the square root of 2 (√2).
Investigating the Square Root of 45
Now, let's focus on the square root of 45 (√45). To determine if it's rational or irrational, we need to try to express it as a fraction p/q. However, we can simplify the problem first.
We can simplify √45 by finding its prime factorization:
45 = 9 x 5 = 3² x 5
Therefore, √45 = √(3² x 5) = √3² x √5 = 3√5
This simplification reveals a crucial element: the presence of √5. The question now becomes: is √5 a rational number?
Proving the Irrationality of √5 (and by extension, 3√5)
To definitively prove that √5 is irrational, we'll employ a common proof technique used for demonstrating the irrationality of square roots of non-perfect squares: proof by contradiction.
1. The Assumption: Let's assume, for the sake of contradiction, that √5 is rational. This means it can be expressed as a fraction p/q, where p and q are integers, q ≠ 0, and the fraction is in its simplest form (meaning p and q have no common factors other than 1).
2. The Equation: If √5 = p/q, then squaring both sides gives us:
5 = p²/q²
3. Rearranging: We can rearrange this equation to:
5q² = p²
This tells us that p² is a multiple of 5. Since 5 is a prime number, this implies that p itself must also be a multiple of 5. We can express this as:
p = 5k, where k is an integer.
4. Substitution: Substituting p = 5k back into the equation 5q² = p², we get:
5q² = (5k)² = 25k²
Dividing both sides by 5, we obtain:
q² = 5k²
This shows that q² is also a multiple of 5, and therefore q must also be a multiple of 5.
5. The Contradiction: We've now shown that both p and q are multiples of 5. This contradicts our initial assumption that p/q is in its simplest form (i.e., they have no common factors). This contradiction means our initial assumption – that √5 is rational – must be false.
6. Conclusion: Therefore, √5 is irrational. Since √45 simplifies to 3√5, and 3 (a rational number) multiplied by an irrational number (√5) results in an irrational number, we can conclude that √45 is irrational.
Deeper Implications and Extensions
This proof highlights a fundamental property of irrational numbers: the square root of any non-perfect square integer is irrational. This extends beyond just √5 and √45. The same proof structure can be used to demonstrate the irrationality of √2, √3, √6, √7, and so on.
The concept of irrationality is crucial in many areas of mathematics, including:
- Geometry: The diagonal of a unit square (√2) is an irrational number, demonstrating that not all lengths can be precisely expressed using rational numbers.
- Calculus: Irrational numbers are essential in defining limits, derivatives, and integrals.
- Number Theory: The study of irrational numbers is a significant branch of number theory, exploring the properties and relationships of these numbers.
- Trigonometry: Many trigonometric functions involve irrational numbers, such as π and the various trigonometric ratios.
Practical Applications and Further Exploration
While the seemingly abstract nature of irrational numbers might seem far removed from daily life, they have numerous practical applications. Consider these examples:
- Construction and Engineering: Precise calculations involving lengths and angles often require dealing with irrational numbers.
- Computer Science: Representing irrational numbers in computer systems involves approximations, leading to considerations of precision and accuracy.
- Physics: Many physical constants and formulas involve irrational numbers, such as the speed of light or gravitational constant.
Understanding irrational numbers like √45 isn't just about theoretical mathematics; it's about gaining a deeper appreciation for the complexity and richness of the number system that underpins our understanding of the world. Further exploration into transcendental numbers (a subset of irrational numbers that are not the root of any polynomial equation with rational coefficients) and continued fractions (an alternative way to represent irrational numbers) can lead to a more profound understanding of this fascinating area of mathematics. The inherent beauty and elegance of irrational numbers invite continued investigation and discovery. The seemingly simple question of whether √45 is rational leads to a surprisingly deep exploration of fundamental mathematical concepts.
Latest Posts
Latest Posts
-
How Many Ml Is 1 75 Liters
Apr 02, 2025
-
Which Of The Following Statement Is False
Apr 02, 2025
-
What Is The Last Element In Period 4
Apr 02, 2025
-
A Sarcomere Is A Regions Between Two
Apr 02, 2025
-
What Percentage Is 1 Out Of 3
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Is The Square Root Of 45 A Rational Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
