Is Mutually Exclusive The Same As Independent
Juapaving
Mar 25, 2025 · 6 min read
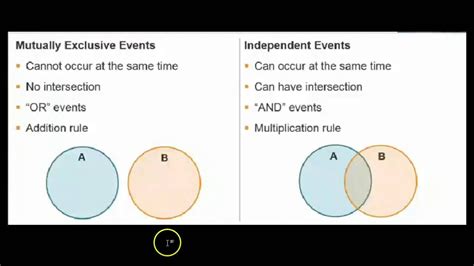
Table of Contents
Is Mutually Exclusive the Same as Independent? Understanding Key Differences in Probability
The terms "mutually exclusive" and "independent" frequently appear in the realm of probability, often causing confusion due to their subtle yet crucial differences. While seemingly interconnected, they represent distinct concepts with unique implications for calculating probabilities. This comprehensive guide will delve into the definitions, explore the key distinctions, and provide illustrative examples to solidify your understanding of these fundamental probabilistic concepts.
Defining Mutually Exclusive Events
Two events are considered mutually exclusive if they cannot both occur simultaneously. In simpler terms, the occurrence of one event automatically precludes the occurrence of the other. Think of it as a situation where only one event can happen at a time. There's no overlap between the events.
Key characteristics of mutually exclusive events:
- No Overlap: The intersection of the events is empty. Using set notation, if A and B are mutually exclusive events, then A ∩ B = Ø (where Ø represents the empty set).
- Conditional Probability: The probability of one event occurring given that the other has already occurred is zero. P(A|B) = P(B|A) = 0.
- Examples:
- Flipping a coin: Getting heads and getting tails are mutually exclusive events. You cannot get both at the same time in a single flip.
- Drawing a card from a deck: Drawing a king and drawing a queen are mutually exclusive events in a single draw.
- Rolling a die: Rolling a 3 and rolling a 6 are mutually exclusive events in a single roll.
Defining Independent Events
Two events are considered independent if the occurrence of one event does not affect the probability of the occurrence of the other event. The outcome of one event has no bearing on the outcome of the other.
Key characteristics of independent events:
- No Influence: The probability of one event remains unchanged regardless of whether the other event has occurred.
- Conditional Probability: The conditional probability of one event given the other is equal to the unconditional probability of that event. That is, P(A|B) = P(A) and P(B|A) = P(B).
- Examples:
- Flipping two coins: The outcome of the first coin flip (heads or tails) does not influence the outcome of the second coin flip.
- Rolling two dice: The result of rolling one die does not affect the result of rolling the other die.
- Drawing cards with replacement: Drawing a king from a deck, replacing it, and then drawing a queen are independent events because the replacement restores the original probability distribution.
The Crucial Difference: Mutually Exclusive vs. Independent
The core difference lies in the relationship between the events:
- Mutually exclusive events focus on the impossibility of simultaneous occurrence. They cannot happen together.
- Independent events focus on the lack of influence one event has on the other. The occurrence of one does not change the likelihood of the other.
This distinction is critical because the formulas for calculating probabilities differ significantly. For mutually exclusive events, the probability of either event occurring is the sum of their individual probabilities: P(A or B) = P(A) + P(B). For independent events, the probability of both events occurring is the product of their individual probabilities: P(A and B) = P(A) * P(B).
Can Events Be Both Mutually Exclusive and Independent?
The answer is largely no, with one important exception. If two events are mutually exclusive, they cannot be independent (unless one or both have a probability of zero). This is because the occurrence of one event completely eliminates the possibility of the other event, directly influencing its probability.
The exception: Consider an event A with P(A) = 0. Event A can be both mutually exclusive and independent with any other event B. This is because if A never occurs, it doesn't influence the occurrence of B. However, this is a trivial case and not usually relevant in practical applications.
Illustrative Examples to Clarify the Difference
Let's solidify the concepts with some examples:
Example 1: Rolling a Die
- Mutually Exclusive: Rolling a 3 and rolling a 6 are mutually exclusive. You cannot roll both a 3 and a 6 on a single roll.
- Independent: Rolling a 3 on the first roll and rolling a 6 on the second roll are independent events. The outcome of the first roll doesn't influence the outcome of the second roll.
Example 2: Drawing Cards
- Mutually Exclusive: Drawing a king and drawing a queen from a deck of cards without replacement are mutually exclusive. If you draw a king, you cannot draw a queen on the same draw.
- Independent: Drawing a king and drawing a queen from a deck of cards with replacement are independent. Replacing the king restores the original probability distribution, so the outcome of the first draw doesn't affect the second.
- Neither Mutually Exclusive nor Independent: Drawing a king and drawing a queen from a deck of cards without replacement are neither mutually exclusive nor independent in the same single draw.
Example 3: Weather and Traffic
- Possibly Independent: The probability of rain and the probability of heavy traffic might be considered independent. Rain doesn't directly cause heavy traffic, although there might be a weak correlation.
- Not Mutually Exclusive: Rain and heavy traffic are not mutually exclusive. It's possible for both to occur simultaneously.
Common Mistakes and Misconceptions
A common mistake is conflating correlation with independence. Correlation describes a statistical relationship between two variables, while independence means one event does not influence the probability of the other. Two events can be correlated without being dependent and vice versa.
Another misconception is assuming that if events are not mutually exclusive, they must be independent. This is incorrect. Many events can be neither mutually exclusive nor independent, as demonstrated in the card example without replacement.
Practical Applications
Understanding the distinction between mutually exclusive and independent events is crucial in various fields:
- Risk Management: Assessing the probability of multiple risks occurring simultaneously.
- Finance: Modeling investment portfolio performance, considering the dependence or independence of different asset classes.
- Medicine: Evaluating the effectiveness of treatments and considering the likelihood of different side effects.
- Machine Learning: Designing algorithms and models that accurately predict probabilities of outcomes based on the independence or dependence of features.
- Quality Control: Determining the probability of defects occurring in a manufacturing process.
Conclusion
Mutually exclusive and independent events are fundamental concepts in probability with significant implications for calculating probabilities and making informed decisions. While seemingly similar, their distinctions are crucial. Mutually exclusive events cannot occur together, while independent events have no influence on each other's probabilities. Mastering these concepts is essential for anyone working with probability and statistics. By carefully examining the nature of the events in question, you can accurately apply the appropriate probability formulas and gain valuable insights. Remember that events can be neither mutually exclusive nor independent, a fact often overlooked. Understanding these subtle differences empowers accurate probability calculations and enhances decision-making across diverse fields.
Latest Posts
Latest Posts
-
How Much Electrons Does Sodium Have
Mar 27, 2025
-
Which Is Larger 3 8 Or 1 2
Mar 27, 2025
-
Which Of The Following Are Not Trigonometric Identities
Mar 27, 2025
-
Why Are Most Ionic Substances Brittle
Mar 27, 2025
-
What Are Examples Of Unit Rates
Mar 27, 2025
Related Post
Thank you for visiting our website which covers about Is Mutually Exclusive The Same As Independent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
