Which Is Larger 3 8 Or 1 2
Juapaving
Mar 27, 2025 · 5 min read
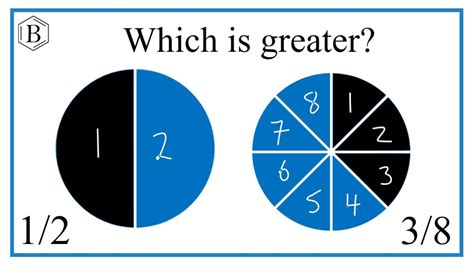
Table of Contents
Which is Larger: 3/8 or 1/2? A Deep Dive into Fraction Comparison
Determining which fraction is larger, 3/8 or 1/2, might seem straightforward at first glance. However, understanding the underlying principles of fraction comparison is crucial for developing a strong foundation in mathematics. This article will not only answer the question but also delve into multiple methods for comparing fractions, offering a comprehensive understanding of this fundamental concept. We'll explore visual representations, equivalent fractions, decimal conversions, and the use of cross-multiplication, providing you with a robust toolkit for tackling similar fraction comparisons in the future.
Understanding Fractions
Before we compare 3/8 and 1/2, let's review the basics of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator shows how many of those parts are being considered.
For instance, in the fraction 3/8, the denominator (8) tells us the whole is divided into eight equal parts, and the numerator (3) indicates we are considering three of those parts. Similarly, in the fraction 1/2, the denominator (2) means the whole is split into two equal parts, and the numerator (1) represents one of those parts.
Visualizing the Fractions
One of the easiest ways to compare fractions is to visualize them. Imagine two identical circles.
Visualizing 1/2
Divide the first circle into two equal halves. Shade one half. This visually represents the fraction 1/2.
Visualizing 3/8
Divide the second circle into eight equal parts. Shade three of those parts. This represents the fraction 3/8.
By visually comparing the shaded portions of both circles, it's immediately apparent that 1/2 is larger than 3/8. The shaded area representing 1/2 is clearly greater than the shaded area representing 3/8. This visual approach offers an intuitive understanding of the comparison, especially for beginners.
Using Equivalent Fractions
Another effective method involves finding equivalent fractions. Equivalent fractions represent the same value but have different numerators and denominators. To find an equivalent fraction, multiply both the numerator and the denominator of a fraction by the same non-zero number.
Let's find an equivalent fraction for 1/2 with a denominator of 8, matching the denominator of 3/8. To achieve this, we multiply both the numerator and denominator of 1/2 by 4:
(1 × 4) / (2 × 4) = 4/8
Now we can easily compare 4/8 and 3/8. Since both fractions share the same denominator, we simply compare their numerators. Clearly, 4/8 is greater than 3/8, confirming that 1/2 is larger than 3/8.
Converting to Decimals
Converting fractions to decimals provides another approach to comparison. To convert a fraction to a decimal, divide the numerator by the denominator.
Converting 1/2 to a Decimal
1 ÷ 2 = 0.5
Converting 3/8 to a Decimal
3 ÷ 8 = 0.375
Comparing the decimal values, 0.5 and 0.375, it's evident that 0.5 (representing 1/2) is larger than 0.375 (representing 3/8). This method provides a numerical comparison, reinforcing the visual and equivalent fraction approaches.
Cross-Multiplication: A More Formal Method
For more complex fraction comparisons, cross-multiplication is a reliable technique. To compare fractions a/b and c/d using cross-multiplication, follow these steps:
- Multiply the numerator of the first fraction (a) by the denominator of the second fraction (d): a × d
- Multiply the numerator of the second fraction (c) by the denominator of the first fraction (b): c × b
- Compare the results:
- If a × d > c × b, then a/b > c/d
- If a × d < c × b, then a/b < c/d
- If a × d = c × b, then a/b = c/d
Let's apply this to our fractions:
- Multiply the numerator of 1/2 by the denominator of 3/8: 1 × 8 = 8
- Multiply the numerator of 3/8 by the denominator of 1/2: 3 × 2 = 6
- Compare the results: 8 > 6, therefore 1/2 > 3/8.
Understanding the Magnitude of the Difference
While we've established that 1/2 is larger than 3/8, it's also beneficial to understand the magnitude of this difference. The difference between 1/2 and 3/8 is:
1/2 - 3/8 = 4/8 - 3/8 = 1/8
This means 1/2 is 1/8 larger than 3/8. Understanding the magnitude of the difference can be crucial in various applications, from cooking to construction, where precise measurements are essential.
Practical Applications of Fraction Comparison
The ability to compare fractions is essential in numerous real-world situations:
- Cooking and Baking: Following recipes often involves working with fractions of cups, teaspoons, and tablespoons.
- Construction and Engineering: Accurate measurements are critical, often involving fractions of inches or meters.
- Finance and Budgeting: Understanding fractions is important when dealing with percentages and proportions of budgets.
- Data Analysis: Fractions are frequently used to represent proportions and ratios in data analysis and statistics.
Conclusion: Mastering Fraction Comparison
Comparing fractions is a fundamental skill in mathematics with wide-ranging practical applications. This article has explored several methods for comparing fractions – visual representation, equivalent fractions, decimal conversion, and cross-multiplication – providing a comprehensive understanding of how to determine which fraction is larger. By mastering these techniques, you'll develop a strong mathematical foundation and enhance your ability to solve problems involving fractions efficiently and accurately. Remember, practicing these methods regularly is key to solidifying your understanding and improving your problem-solving skills. The ability to confidently compare fractions is a valuable asset in various fields and everyday life. So, next time you encounter a fraction comparison, you'll be well-equipped to tackle it with confidence!
Latest Posts
Latest Posts
-
Write 72 As A Product Of Prime Factors
Mar 30, 2025
-
How To Find The Latus Rectum Of A Parabola
Mar 30, 2025
-
Greatest Common Factor Of 24 And 30
Mar 30, 2025
-
What Are All Of The Factors Of 49
Mar 30, 2025
-
Lowest Common Factor Of 3 And 8
Mar 30, 2025
Related Post
Thank you for visiting our website which covers about Which Is Larger 3 8 Or 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
