Is 7 A Factor Of 84
Juapaving
Mar 24, 2025 · 4 min read
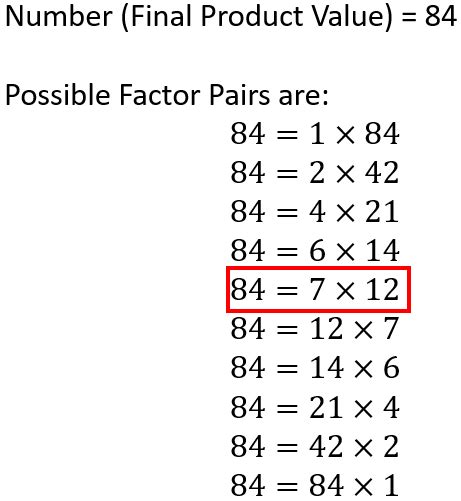
Table of Contents
Is 7 a Factor of 84? A Deep Dive into Divisibility and Factors
This article explores the question, "Is 7 a factor of 84?" We'll delve into the concept of factors, divisibility rules, and different methods to determine if one number is a factor of another. We will also touch upon related mathematical concepts and provide examples to solidify understanding. This comprehensive guide aims to provide a clear and thorough answer, suitable for various levels of mathematical understanding.
Understanding Factors and Divisibility
Before diving into whether 7 is a factor of 84, let's define some key terms:
-
Factors: Factors of a number are whole numbers that divide the number exactly, leaving no remainder. For instance, the factors of 12 are 1, 2, 3, 4, 6, and 12.
-
Divisibility: Divisibility refers to the ability of a number to be divided by another number without leaving a remainder. If a number is divisible by another, the second number is a factor of the first.
-
Prime Factorization: This is the process of expressing a number as a product of its prime factors. Prime factors are whole numbers greater than 1 that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11...). Prime factorization is a powerful tool for finding factors and simplifying mathematical operations.
Method 1: Direct Division
The most straightforward method to determine if 7 is a factor of 84 is to perform the division: 84 ÷ 7.
84 ÷ 7 = 12
Since the division results in a whole number (12) with no remainder, we can definitively conclude that yes, 7 is a factor of 84.
Method 2: Prime Factorization
Prime factorization offers a more insightful approach. Let's find the prime factorization of 84:
84 = 2 x 42 = 2 x 2 x 21 = 2 x 2 x 3 x 7
The prime factorization of 84 is 2² x 3 x 7. Notice that 7 appears as one of the prime factors. This clearly shows that 7 is a factor of 84. This method not only confirms that 7 is a factor but also reveals the other factors of 84.
Method 3: Divisibility Rules
While direct division is simple for smaller numbers, divisibility rules can be helpful for larger numbers. Although there isn't a specific divisibility rule for 7 that is as straightforward as those for 2, 3, 5, or 10, we can still use the concept of divisibility to approach the problem. Since we already know that 84 ÷ 7 = 12, we can demonstrate the principle of divisibility. Because the division yields an integer (12) without any remainder, it satisfies the definition of divisibility and confirms that 7 is a factor.
Exploring Further: Factors of 84
Now that we've established that 7 is a factor of 84, let's explore the complete set of factors for 84:
Using the prime factorization (2² x 3 x 7), we can systematically identify all factors:
- 1: Every number has 1 as a factor.
- 2: From the prime factorization.
- 3: From the prime factorization.
- 4: 2 x 2 = 2²
- 6: 2 x 3
- 7: From the prime factorization.
- 12: 2² x 3
- 14: 2 x 7
- 21: 3 x 7
- 28: 2² x 7
- 42: 2 x 3 x 7
- 84: The number itself is always a factor.
Therefore, the factors of 84 are 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, and 84.
Practical Applications of Finding Factors
Understanding factors and divisibility is crucial in various mathematical applications, including:
-
Simplifying Fractions: Finding the greatest common factor (GCF) of the numerator and denominator allows for simplifying fractions to their lowest terms.
-
Solving Equations: Factorization is a vital technique in solving algebraic equations and simplifying expressions.
-
Number Theory: Factorization plays a key role in many number theory concepts, such as prime numbers, perfect numbers, and abundant numbers.
-
Cryptography: Factorization is fundamental to certain types of cryptography, where the security relies on the difficulty of factoring large numbers.
Advanced Concepts Related to Divisibility
Beyond the basic concepts, more advanced mathematical ideas relate to divisibility:
-
Modular Arithmetic: This system deals with remainders after division, providing a powerful tool for analyzing divisibility and solving problems involving congruences.
-
Greatest Common Divisor (GCD): The GCD of two or more numbers is the largest number that divides all of them without leaving a remainder. Algorithms like the Euclidean algorithm efficiently compute the GCD.
-
Least Common Multiple (LCM): The LCM of two or more numbers is the smallest number that is a multiple of all of them.
Conclusion: 7 is Indeed a Factor of 84
Through direct division, prime factorization, and a discussion of divisibility, we have conclusively demonstrated that 7 is a factor of 84. Understanding factors and divisibility is a fundamental skill in mathematics with applications across various fields. This exploration provided not only the answer but also a broader understanding of related mathematical concepts, enhancing your overall mathematical knowledge. Remember, mastering these concepts will improve your problem-solving skills and your ability to tackle more complex mathematical challenges. The ability to easily identify factors is a valuable asset in various mathematical contexts, making it a key skill to develop.
Latest Posts
Latest Posts
-
What Is A Solution And A Mixture
Mar 28, 2025
-
What Is The Electron Configuration For Rb
Mar 28, 2025
-
What Is 25 Percent Of 150
Mar 28, 2025
-
Which Of The Following Energy Sources Drives The Hydrologic Cycle
Mar 28, 2025
-
How Many Sides Has A Rectangle
Mar 28, 2025
Related Post
Thank you for visiting our website which covers about Is 7 A Factor Of 84 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
