Is 3 8 Smaller Than 1 2
Juapaving
Mar 21, 2025 · 5 min read
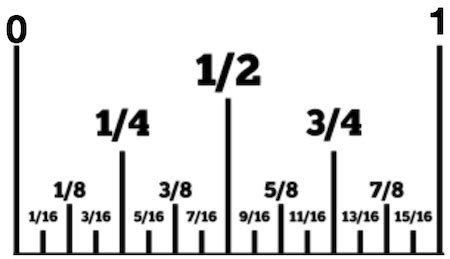
Table of Contents
Is 3/8 Smaller Than 1/2? A Deep Dive into Fraction Comparison
The question, "Is 3/8 smaller than 1/2?", might seem trivial at first glance. However, understanding how to compare fractions is a fundamental skill in mathematics with far-reaching applications in various fields. This article will not only answer this specific question definitively but also explore various methods for comparing fractions, providing you with a comprehensive understanding of the subject. We'll delve into the intricacies of fraction manipulation, demonstrating multiple approaches to ensure you can confidently compare any two fractions.
Understanding Fractions: A Quick Refresher
Before we tackle the core question, let's refresh our understanding of what a fraction represents. A fraction, such as 3/8, consists of two key parts:
- Numerator: The top number (3 in this case) represents the number of parts you have.
- Denominator: The bottom number (8 in this case) represents the total number of equal parts the whole is divided into.
Therefore, 3/8 signifies that you possess 3 out of 8 equal parts of a whole. Similarly, 1/2 represents 1 out of 2 equal parts.
Method 1: Finding a Common Denominator
The most straightforward method for comparing fractions involves finding a common denominator. This means converting both fractions so they share the same denominator. Once they have the same denominator, you can simply compare their numerators.
Steps:
-
Find the least common multiple (LCM) of the denominators: The denominators are 8 and 2. The LCM of 8 and 2 is 8.
-
Convert the fractions to equivalent fractions with the common denominator:
- 3/8 already has a denominator of 8, so it remains as 3/8.
- To convert 1/2 to an equivalent fraction with a denominator of 8, multiply both the numerator and denominator by 4: (1 * 4) / (2 * 4) = 4/8.
-
Compare the numerators: Now we compare 3/8 and 4/8. Since 3 < 4, we conclude that 3/8 < 4/8, and therefore, 3/8 < 1/2.
Method 2: Converting Fractions to Decimals
Another effective method for comparing fractions is to convert them into their decimal equivalents. This approach is particularly useful when dealing with fractions that are difficult to compare directly using a common denominator.
Steps:
-
Convert each fraction to a decimal:
- 3/8 = 0.375
- 1/2 = 0.5
-
Compare the decimals: Since 0.375 < 0.5, we can definitively say that 3/8 < 1/2.
This method offers a clear visual comparison, making it easy to understand the relative sizes of the fractions.
Method 3: Visual Representation (Using a Diagram)
A visual approach can be particularly helpful for grasping the concept of fraction comparison, especially for those who are more visually oriented learners.
Imagine a circle divided into 8 equal parts. Shading 3 of these parts represents 3/8. Now, imagine another circle divided into 2 equal parts. Shading one of these parts represents 1/2. Visually comparing the shaded areas clearly shows that the shaded area representing 3/8 is smaller than the shaded area representing 1/2.
This visual method, while not as mathematically rigorous as the previous two, provides an intuitive understanding of the size comparison.
Expanding on Fraction Comparison Techniques: Advanced Concepts
While the methods above are sufficient for comparing simple fractions like 3/8 and 1/2, more sophisticated techniques are necessary for handling more complex scenarios. Let's explore some of these:
1. Cross-Multiplication: This method is particularly useful when dealing with fractions that are not easily converted to a common denominator.
Steps:
-
Cross-multiply the numerators and denominators: Multiply the numerator of the first fraction by the denominator of the second fraction, and vice-versa.
- 3/8 and 1/2: (3 * 2) = 6 and (8 * 1) = 8
-
Compare the products: The result of the cross-multiplication gives you two numbers to compare. The fraction with the smaller product on the left is the smaller fraction.
- Since 6 < 8, we conclude that 3/8 < 1/2.
2. Using a Number Line: Placing fractions on a number line provides a visual representation of their relative positions and values. This method is particularly helpful for visualizing the order of fractions.
3. Converting Improper Fractions and Mixed Numbers: If you are comparing improper fractions (where the numerator is larger than the denominator) or mixed numbers (a whole number and a fraction), you will first need to convert them into a consistent format, either all improper fractions or all mixed numbers, before using any of the above methods.
Real-World Applications of Fraction Comparison
The ability to compare fractions is not merely an academic exercise; it has practical applications in various real-world scenarios:
- Cooking and Baking: Following recipes often requires understanding and comparing fractional measurements of ingredients.
- Construction and Engineering: Precise measurements in construction and engineering rely heavily on the accurate comparison of fractions.
- Financial Calculations: Understanding fractions is crucial for calculating percentages, interest rates, and other financial metrics.
- Data Analysis: In many fields, data is presented in fractional form, and the ability to compare these fractions is essential for interpretation and analysis.
Conclusion: Mastering Fraction Comparison
The question, "Is 3/8 smaller than 1/2?", has led us on a journey exploring various methods for comparing fractions. We've established definitively that yes, 3/8 is indeed smaller than 1/2. However, the true value of this exploration lies in gaining a deeper understanding of the techniques involved. Whether you use the common denominator method, decimal conversion, visual representation, or cross-multiplication, mastering these skills equips you with a powerful tool for tackling more complex mathematical problems and real-world applications involving fractions. Remember, the choice of method often depends on the specific fractions involved and your personal preference. Practice is key to developing fluency and confidence in comparing fractions.
Latest Posts
Latest Posts
-
The Role Of The Light Harvesting Complex Is To
Mar 28, 2025
-
Electrical Conductivity Physical Or Chemical Property
Mar 28, 2025
-
Why Do Atoms Want 8 Valence Electrons
Mar 28, 2025
-
Two Angles Whose Measures Have A Sum Of 180 Degrees
Mar 28, 2025
-
Select All Of The Following That Are Characteristics Of Plants
Mar 28, 2025
Related Post
Thank you for visiting our website which covers about Is 3 8 Smaller Than 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
