Intermediate Value Theorem Vs Mean Value Theorem
Juapaving
Mar 21, 2025 · 6 min read
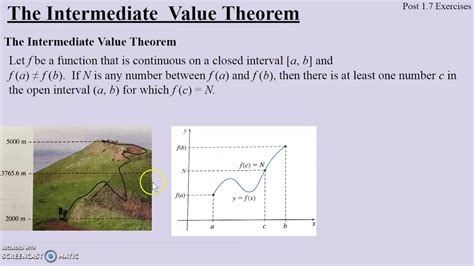
Table of Contents
- Intermediate Value Theorem Vs Mean Value Theorem
- Table of Contents
- Intermediate Value Theorem vs. Mean Value Theorem: A Deep Dive
- Understanding the Intermediate Value Theorem (IVT)
- Deconstructing the Mean Value Theorem (MVT)
- Key Differences and Similarities
- Applications and Implications
- Advanced Considerations and Extensions
- Conclusion
- Latest Posts
- Latest Posts
- Related Post
Intermediate Value Theorem vs. Mean Value Theorem: A Deep Dive
Both the Intermediate Value Theorem (IVT) and the Mean Value Theorem (MVT) are cornerstones of calculus, offering crucial insights into the behavior of continuous functions. While seemingly disparate at first glance, understanding their differences and interrelationships is key to mastering calculus and its applications. This article provides a comprehensive comparison of the IVT and MVT, exploring their statements, proofs, applications, and subtle distinctions.
Understanding the Intermediate Value Theorem (IVT)
The IVT, in essence, states that a continuous function must take on every value between any two of its values. More formally:
Statement: If f is a continuous function on the closed interval [a, b], and k is any number between f(a) and f(b), then there exists at least one number c in the open interval (a, b) such that f(c) = k.
Intuitive Explanation: Imagine drawing a continuous curve between two points on a graph. The IVT guarantees that the curve must cross every horizontal line between the y-coordinates of those two points at least once. There's no way to "jump" over a value without creating a discontinuity.
Proof (Sketch): The proof typically utilizes the completeness property of real numbers and involves constructing a sequence of nested intervals that converge to a point c satisfying f(c) = k. The continuity of f ensures that this convergence leads to the desired result. A rigorous proof involves concepts beyond the scope of this introductory explanation but can be found in most advanced calculus textbooks.
Example: Consider the function f(x) = x² on the interval [-1, 2]. f(-1) = 1 and f(2) = 4. If k = 2, the IVT guarantees the existence of a c in (-1, 2) such that f(c) = 2. In this case, c = √2.
Deconstructing the Mean Value Theorem (MVT)
The MVT, unlike the IVT, deals with the rate of change of a function. It connects the average rate of change over an interval to the instantaneous rate of change at some point within that interval.
Statement: If f is a continuous function on the closed interval [a, b] and differentiable on the open interval (a, b), then there exists at least one number c in (a, b) such that:
f'(c) = (f(b) - f(a)) / (b - a)
Intuitive Explanation: The expression (f(b) - f(a)) / (b - a) represents the average rate of change of f over the interval [a, b] (the slope of the secant line connecting the points (a, f(a)) and (b, f(b))). The MVT states that there's at least one point c in the interval where the instantaneous rate of change (the slope of the tangent line at c) is equal to this average rate of change. Geometrically, this means there exists a tangent line parallel to the secant line connecting the endpoints.
Proof (Sketch): The proof relies on Rolle's Theorem, a special case of the MVT where f(a) = f(b). By constructing an auxiliary function that incorporates the average rate of change, Rolle's Theorem can be applied to deduce the existence of c satisfying the MVT's condition. Again, a detailed proof can be found in standard calculus resources.
Example: Consider the function f(x) = x³ on the interval [0, 2]. f(0) = 0 and f(2) = 8. The average rate of change is (8 - 0) / (2 - 0) = 4. The MVT guarantees the existence of a c in (0, 2) such that f'(c) = 4. Since f'(x) = 3x², we have 3c² = 4, which gives c = 2/√3.
Key Differences and Similarities
While both theorems deal with continuous functions, their core focuses differ significantly:
| Feature | Intermediate Value Theorem (IVT) | Mean Value Theorem (MVT) |
|---|---|---|
| Focus | Existence of intermediate values of the function | Existence of a point with specific derivative |
| Requirement | Continuity on [a, b] | Continuity on [a, b] and differentiability on (a, b) |
| Conclusion | Existence of c such that f(c) = k | Existence of c such that f'(c) = (f(b) - f(a)) / (b - a) |
| Geometric Interpretation | Curve crosses every horizontal line between f(a) and f(b) | Tangent line parallel to secant line |
Similarities:
- Both theorems guarantee the existence of a point c within the interval (a, b). They don't provide a method for finding c, only its existence.
- Both theorems are fundamental to many proofs and applications in calculus and analysis.
- Both theorems require the function to be continuous on the closed interval [a, b]. The MVT adds the requirement of differentiability on the open interval (a, b).
Applications and Implications
The IVT and MVT have far-reaching consequences in various fields:
Intermediate Value Theorem Applications:
- Finding roots: The IVT is crucial in proving the existence of roots for continuous functions. If a continuous function changes sign on an interval, the IVT guarantees at least one root within that interval. This forms the basis of numerical root-finding methods like the Bisection Method.
- Showing existence of solutions: Many problems in physics, engineering, and economics can be modeled using equations that involve continuous functions. The IVT can be used to demonstrate the existence of solutions to these equations within a certain range.
- Establishing properties of functions: The IVT helps in establishing certain properties of continuous functions, such as proving that a continuous function on a closed interval attains its maximum and minimum values.
Mean Value Theorem Applications:
- Optimization problems: The MVT is instrumental in finding optimal solutions in various applications. By analyzing the derivative, we can locate critical points and determine whether they correspond to maxima, minima, or saddle points.
- Physics: The MVT plays a significant role in physics, especially in kinematics. It relates the average velocity to the instantaneous velocity at some point in time.
- Error analysis: In numerical analysis, the MVT is used to bound errors in approximations and numerical methods. It provides a way to estimate how much the approximation deviates from the true value.
- Taylor's Theorem: The MVT is a crucial stepping stone in the proof of Taylor's Theorem, a powerful tool for approximating functions using polynomials.
Advanced Considerations and Extensions
Beyond the basic theorems, several extensions and related concepts exist:
- Generalized Mean Value Theorem (Cauchy's Mean Value Theorem): This extends the MVT to involve two functions, providing a more general relationship between their average and instantaneous rates of change.
- Higher-order Mean Value Theorems: These extend the MVT to higher-order derivatives, providing increasingly precise approximations of functions.
Conclusion
The Intermediate Value Theorem and the Mean Value Theorem, while distinct in their statements and applications, are both indispensable tools in the realm of calculus. The IVT guarantees the existence of intermediate values for continuous functions, while the MVT establishes a relationship between average and instantaneous rates of change. Both theorems underpin many important results and applications across various disciplines, highlighting their fundamental significance in mathematical analysis and its practical applications. A thorough understanding of these theorems is essential for anyone pursuing a deeper understanding of calculus and its applications.
Latest Posts
Latest Posts
-
What Is The Square Root Of One
Mar 28, 2025
-
How Many Lines Of Symmetry Does An Isosceles Trapezium Have
Mar 28, 2025
-
What Is All The Factors Of 49
Mar 28, 2025
-
How Many Lines Of Symmetry In A Star
Mar 28, 2025
-
Higher Level Languages Vs Assembly Language
Mar 28, 2025
Related Post
Thank you for visiting our website which covers about Intermediate Value Theorem Vs Mean Value Theorem . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
