How Many Lines Of Symmetry Does An Isosceles Trapezium Have
Juapaving
Mar 28, 2025 · 5 min read
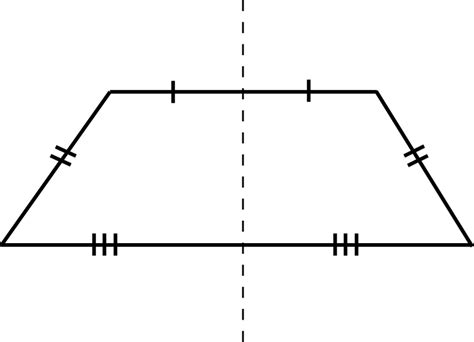
Table of Contents
How Many Lines of Symmetry Does an Isosceles Trapezium Have? A Comprehensive Exploration
Understanding lines of symmetry is fundamental in geometry, allowing us to analyze shapes and their properties. This article delves deep into the fascinating world of isosceles trapeziums and their symmetry, answering the question: how many lines of symmetry does an isosceles trapezium have? We'll explore the definition, properties, and characteristics of isosceles trapeziums, ultimately providing a clear and definitive answer, supported by visual aids and logical reasoning.
Defining an Isosceles Trapezium
Before we delve into lines of symmetry, let's establish a firm understanding of what constitutes an isosceles trapezium. An isosceles trapezium (also known as an isosceles trapezoid) is a quadrilateral with:
- Two parallel sides: These parallel sides are called the bases of the trapezium.
- Two non-parallel sides of equal length: These equal sides are often referred to as the legs.
It's crucial to differentiate an isosceles trapezium from a general trapezium. A general trapezium simply possesses two parallel sides, without any restrictions on the lengths of the non-parallel sides. The defining characteristic of an isosceles trapezium is the equality of its legs. This equality introduces a unique symmetry not found in general trapeziums.
Lines of Symmetry: A Fundamental Concept
A line of symmetry (also known as a line of reflection or axis of symmetry) divides a shape into two identical halves that are mirror images of each other. If you were to fold the shape along the line of symmetry, the two halves would perfectly overlap. Shapes can have multiple lines of symmetry, zero lines of symmetry, or even an infinite number (like a circle).
Exploring the Symmetry of an Isosceles Trapezium
Now, let's address the central question: how many lines of symmetry does an isosceles trapezium possess? The answer, unequivocally, is one.
To understand why, let's consider the properties of an isosceles trapezium:
-
Base Angles are Equal: In an isosceles trapezium, the angles at the ends of each base are equal. This means that the angles adjacent to the longer base are equal to each other, and similarly, the angles adjacent to the shorter base are equal to each other. This equality of angles is a direct consequence of the equal lengths of the legs.
-
The Line Connecting Midpoints of the Bases: A line drawn connecting the midpoints of the two parallel sides (bases) of the isosceles trapezium is a line of symmetry. This line is perpendicular to both bases, bisecting the trapezium into two congruent mirror images. Folding the trapezium along this line would perfectly overlap the two halves.
Visualizing the Single Line of Symmetry:
Imagine an isosceles trapezium drawn on a piece of paper. You can only fold it along one specific line to obtain two perfectly overlapping halves. This line passes through the midpoints of both bases and is perpendicular to them. Trying to fold it along any other line will not result in perfectly overlapping halves, confirming the existence of only one line of symmetry.
Comparing to Other Quadrilaterals
Understanding the number of lines of symmetry in an isosceles trapezium becomes clearer when compared to other quadrilaterals:
- Rectangle: A rectangle possesses two lines of symmetry—one horizontal and one vertical.
- Square: A square, a special case of a rectangle, boasts four lines of symmetry—two diagonals and two lines bisecting opposite sides.
- Rhombus: A rhombus has two lines of symmetry—its diagonals.
- Kite: A kite generally has one line of symmetry, the diagonal connecting the vertices of the two pairs of equal sides. A special case is a rhombus.
Mathematical Proof of Single Line of Symmetry
Let's consider a more rigorous approach to proving the isosceles trapezium has only one line of symmetry. We can use coordinate geometry:
Let's define the coordinates of an isosceles trapezium ABCD, where AB is parallel to CD. Let A = (0, a), B = (b, a), C = (d, 0), and D = (c, 0). Due to the isosceles nature, the lengths AD and BC are equal. Therefore:
√[(c-0)² + (0-a)²] = √[(d-b)² + (0-a)²]
Simplifying this equation, we find:
c² + a² = (d-b)² + a²
c² = (d-b)²
c = d - b or c = b - d
This shows a relationship between the x-coordinates defining the parallel bases and demonstrates the symmetry. The perpendicular bisector of both bases would serve as the single line of symmetry. Any other line of reflection would not result in congruent images.
Applications and Real-World Examples
The understanding of lines of symmetry, particularly in isosceles trapeziums, has applications in various fields:
-
Architecture and Design: Architects and designers often utilize symmetrical shapes, including isosceles trapeziums, to create visually appealing and balanced structures. This is particularly relevant in designing aesthetically pleasing buildings, bridges, and other structures.
-
Engineering: In engineering, understanding symmetry is vital for designing stable and efficient structures. Symmetrical designs often provide better load distribution and structural integrity.
-
Art and Graphics: Artists and graphic designers also use symmetry in their artwork to create visually pleasing and balanced compositions. Understanding the unique symmetry of an isosceles trapezium can enhance creative design.
-
Computer Graphics and Game Development: Symmetry is a key concept in computer graphics and game development for creating efficient and visually appealing models and environments.
Conclusion: One Line, Many Applications
In conclusion, an isosceles trapezium possesses only one line of symmetry, the line connecting the midpoints of its parallel sides. This unique characteristic distinguishes it from other quadrilaterals and underscores its specific geometric properties. While having only one line of symmetry might seem less visually striking than the multiple lines of symmetry in a square, its application across different fields showcases its importance in various disciplines. Understanding this fundamental aspect of its geometry enhances our comprehension of shapes and their application in the real world. The single line of symmetry in an isosceles trapezium is a testament to the beauty and precision of geometrical principles.
Latest Posts
Latest Posts
-
How Many Cm Is 36 Inches
Mar 31, 2025
-
Is Oxygen A Metal Or Nonmetal
Mar 31, 2025
-
72 As Product Of Prime Factors
Mar 31, 2025
-
How Many Valence Electrons Does S2 Have
Mar 31, 2025
-
What Is 17 25 As A Decimal
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about How Many Lines Of Symmetry Does An Isosceles Trapezium Have . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
