How Many Lines Of Symmetry In A Star
Juapaving
Mar 28, 2025 · 5 min read
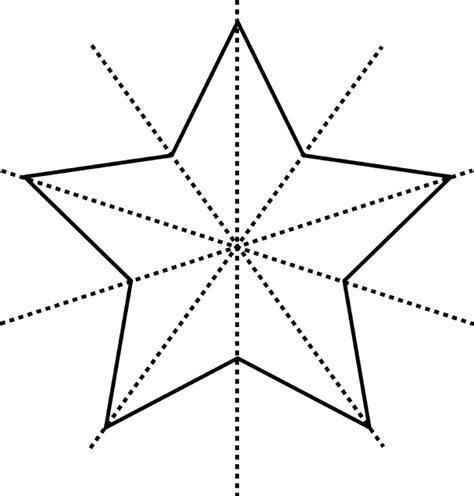
Table of Contents
How Many Lines of Symmetry in a Star? Exploring the Geometry of Stars
The seemingly simple question, "How many lines of symmetry does a star have?" unveils a surprisingly rich exploration into geometry, specifically focusing on rotational and reflectional symmetry. The answer, however, isn't a single number but depends entirely on the type of star we're examining. This article delves into the different types of star shapes, their lines of symmetry, and the mathematical principles behind them. We'll explore regular stars, irregular stars, and even consider the symmetries found in real-world celestial stars, moving beyond the idealized geometric representations.
Understanding Symmetry: Reflectional and Rotational Symmetry
Before diving into the specifics of star shapes, let's establish a firm understanding of symmetry. Symmetry, in a geometric context, refers to a property of an object that remains unchanged under certain transformations. Two key types of symmetry are relevant to our discussion:
Reflectional Symmetry (Line Symmetry)
Reflectional symmetry, also known as line symmetry or bilateral symmetry, occurs when an object can be folded along a line (the axis of symmetry) such that the two halves are mirror images of each other. The line of symmetry divides the object into two congruent halves. Think of a butterfly; it has one line of symmetry down the center.
Rotational Symmetry
Rotational symmetry, also called radial symmetry, exists when an object can be rotated about a central point (the center of rotation) by a certain angle and still appear unchanged. The angle of rotation is a fraction of 360 degrees, and the number of times the object maps onto itself during a full 360-degree rotation determines the order of rotational symmetry. A square, for example, has rotational symmetry of order 4 because it maps onto itself four times during a 360-degree rotation (every 90 degrees).
Lines of Symmetry in Regular Stars
Regular stars are geometric shapes constructed by connecting vertices of a regular polygon in a specific pattern. The number of points (cusps) and the pattern of connections determine the number of lines of symmetry. A crucial factor influencing the symmetry is the number of points (n) and the method of connection (connecting every kth point where k is a factor of n but k < n/2).
Let's consider some examples:
Five-Pointed Star (Pentagram)
The classic five-pointed star, also known as a pentagram, holds a special place in geometry and symbolism. It exhibits both reflectional and rotational symmetry.
-
Reflectional Symmetry: A five-pointed star possesses five lines of symmetry. These lines pass through each point and the midpoint of the opposite edge.
-
Rotational Symmetry: It has rotational symmetry of order 5, meaning it can be rotated by 72 degrees (360/5) and still look identical.
Six-Pointed Star (Hexagram)
The six-pointed star, often depicted as two overlapping equilateral triangles, possesses a higher degree of symmetry than the pentagram.
-
Reflectional Symmetry: A six-pointed star has six lines of symmetry. Three lines connect opposite points, and three lines connect midpoints of opposite sides.
-
Rotational Symmetry: It exhibits rotational symmetry of order 6 (rotations of 60 degrees).
Eight-Pointed Star (Octagram)
An eight-pointed star, depending on its construction, can have varying symmetries. If constructed correctly, it can display a higher degree of symmetry.
-
Reflectional Symmetry: A regular eight-pointed star can have eight lines of symmetry.
-
Rotational Symmetry: It will possess rotational symmetry of order 8.
Generalizing for n-Pointed Stars
For a regular n-pointed star constructed by connecting every kth point (where k and n are coprime and k < n/2), the number of lines of symmetry is generally n. However, this is a simplification and doesn't account for all possible star constructions. Some constructions might lead to fewer lines of symmetry.
Lines of Symmetry in Irregular Stars
Unlike regular stars, irregular stars lack the precise geometric relationships of their regular counterparts. They don't necessarily have the same length of arms or angles between arms. Consequently, the number of lines of symmetry in an irregular star can vary greatly. It could have:
-
Zero lines of symmetry: Most irregular stars will not possess any lines of symmetry.
-
One or more lines of symmetry: In rare cases, an irregular star might exhibit one or more lines of reflectional symmetry, but this is less common. The presence of symmetry would depend on the specific arrangement of points and the lengths of the arms.
Real-World Stars and Symmetry
When considering actual stars in the night sky, the concept of symmetry is not directly applicable in the same geometrical sense. Real stars are massive, complex celestial bodies with incredibly intricate internal structures and magnetic fields. While they might possess approximate spherical symmetry due to gravitational forces, the notion of lines of symmetry is not physically meaningful for them.
Applications and Further Exploration
The study of symmetry in star shapes extends beyond mere geometric curiosity. It has applications in:
-
Design and Art: The aesthetic appeal of stars in various cultural designs and artistic creations directly relates to their inherent symmetry.
-
Crystallography: Symmetry principles are crucial in understanding crystal structures, and some crystal forms bear a resemblance to star shapes.
-
Computer Graphics: The generation of star shapes in computer graphics relies heavily on understanding their geometric properties, including their symmetry.
Conclusion
The number of lines of symmetry in a star is not a universally fixed number but varies depending on its type and construction. Regular stars, with their precise geometric arrangements, typically possess a number of lines of symmetry equal to the number of points. However, irregular stars lack such regularity and usually have fewer or no lines of symmetry. While real celestial stars defy simplistic geometric models of symmetry, the mathematical exploration of star shapes and their symmetries remains a fascinating aspect of geometry with various applications in different fields. Understanding the principles of rotational and reflectional symmetry is essential for appreciating the intricacies and beauty found in these geometric figures. This deeper understanding opens doors to further exploration in areas like advanced geometric constructions and their symbolic representations across cultures and throughout history.
Latest Posts
Latest Posts
-
How Many Cm Is 36 Inches
Mar 31, 2025
-
Is Oxygen A Metal Or Nonmetal
Mar 31, 2025
-
72 As Product Of Prime Factors
Mar 31, 2025
-
How Many Valence Electrons Does S2 Have
Mar 31, 2025
-
What Is 17 25 As A Decimal
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about How Many Lines Of Symmetry In A Star . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
