How To Find Ph Given Pka
Juapaving
Apr 01, 2025 · 6 min read
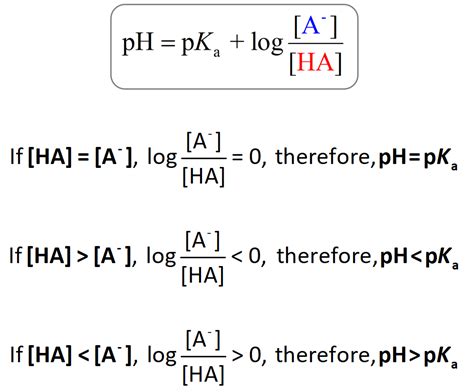
Table of Contents
How to Find pH Given pKa: A Comprehensive Guide
Determining the pH of a solution given its pKa is a fundamental concept in chemistry, particularly crucial in various fields like biochemistry, environmental science, and chemical engineering. Understanding this relationship allows us to predict the behavior of acids and bases in different environments. This comprehensive guide will delve into the methods for calculating pH given pKa, exploring various scenarios and providing practical examples to solidify your understanding.
Understanding the Basics: pH, pKa, and the Henderson-Hasselbalch Equation
Before diving into the calculations, let's refresh our understanding of some key concepts:
-
pH: The pH of a solution is a measure of its acidity or basicity, represented by the negative logarithm (base 10) of the hydrogen ion concentration ([H+]): pH = -log₁₀[H+]. A lower pH indicates a more acidic solution, while a higher pH indicates a more basic solution. A pH of 7 is considered neutral at 25°C.
-
pKa: The pKa is a measure of the acidity of a substance. It represents the negative logarithm (base 10) of the acid dissociation constant (Ka): pKa = -log₁₀Ka. A lower pKa value indicates a stronger acid, meaning it readily donates protons (H+).
-
Ka (Acid Dissociation Constant): This equilibrium constant represents the extent to which an acid dissociates in water. A higher Ka value indicates a stronger acid. For a generic weak acid, HA, the dissociation reaction is: HA ⇌ H+ + A-. The Ka is expressed as: Ka = [H+][A-] / [HA].
The cornerstone for calculating pH from pKa is the Henderson-Hasselbalch equation:
pH = pKa + log₁₀([A-]/[HA])
This equation is applicable to buffer solutions, which are solutions that resist changes in pH upon the addition of small amounts of acid or base. The equation relates the pH of a buffer solution to the pKa of the weak acid and the ratio of the concentrations of the conjugate base ([A-]) and the weak acid ([HA]).
Calculating pH Given pKa: Different Scenarios
The method for calculating pH from pKa varies depending on the specific scenario:
Scenario 1: Calculating pH of a Buffer Solution
This is the most common application of the Henderson-Hasselbalch equation. You are given the pKa of the weak acid and the concentrations of both the weak acid and its conjugate base.
Example:
A buffer solution is prepared by mixing 0.10 M acetic acid (CH₃COOH) and 0.20 M sodium acetate (CH₃COONa). The pKa of acetic acid is 4.76. Calculate the pH of the buffer solution.
Solution:
-
Identify the components: CH₃COOH is the weak acid (HA), and CH₃COONa is its conjugate base (A-).
-
Apply the Henderson-Hasselbalch equation:
pH = pKa + log₁₀([A-]/[HA]) = 4.76 + log₁₀(0.20 M / 0.10 M) = 4.76 + log₁₀(2) ≈ 4.76 + 0.30 = 5.06
Therefore, the pH of the buffer solution is approximately 5.06.
Scenario 2: Calculating pH of a Weak Acid Solution
If you only have the concentration of a weak acid and its pKa, you need to use an iterative approach or approximation methods. The exact calculation involves solving a quadratic equation, but an approximation can often be used if the acid is weak (meaning it doesn't dissociate much).
Example:
Calculate the pH of a 0.10 M solution of benzoic acid (C₆H₅COOH), which has a pKa of 4.20.
Solution:
-
Approximation Method (assuming minimal dissociation):
Since benzoic acid is a weak acid, we can assume that the concentration of H+ ([H+]) is significantly less than the initial concentration of the acid (0.10 M). Therefore, we can simplify the Ka expression:
Ka = [H+][A-]/[HA] ≈ [H+]²/[HA]
We can calculate Ka from pKa: Ka = 10⁻⁴·²⁰ ≈ 6.31 x 10⁻⁵
Now we can solve for [H+]:
6.31 x 10⁻⁵ = [H+]²/0.10 => [H+] = √(6.31 x 10⁻⁶) ≈ 2.51 x 10⁻³ M
Then calculate pH:
pH = -log₁₀(2.51 x 10⁻³) ≈ 2.60
-
Quadratic Equation Method (more accurate):
For greater accuracy, especially if the acid is not very weak or the concentration is high, we need to use the quadratic formula:
Ka = [H+]²/[HA] - [H+]
Substituting the values and solving the quadratic equation:
6.31 x 10⁻⁵ = x²/(0.10 - x)
Where 'x' represents [H+]. Solving this equation (using the quadratic formula) will give a more precise value for [H+], leading to a slightly more accurate pH. This will generally yield a pH value close but not exactly the same as from the approximation method.
Scenario 3: Calculating pH of a Strong Acid Solution
For strong acids, which completely dissociate in water, the calculation is straightforward. The concentration of H+ is directly equal to the concentration of the strong acid.
Example:
Calculate the pH of a 0.01 M solution of hydrochloric acid (HCl), a strong acid.
Solution:
Since HCl is a strong acid, it completely dissociates: HCl → H+ + Cl-. Therefore, [H+] = 0.01 M.
pH = -log₁₀(0.01 M) = 2
Scenario 4: Calculating pH of a Polyprotic Acid Solution
Polyprotic acids have more than one ionizable proton. Calculating the pH requires considering the stepwise dissociation of each proton. The first dissociation will usually contribute most significantly to the overall pH, however, depending on the pKa values and concentration, the contribution of the second or subsequent dissociations might also be significant and cannot be neglected. For such calculations, iterative methods or numerical approaches are usually required.
Advanced Considerations and Applications
The Henderson-Hasselbalch equation and the methods described above offer valuable tools for understanding and predicting the pH of solutions containing weak acids and their conjugate bases. However, several factors may affect the accuracy and applicability of these methods in real-world scenarios:
-
Ionic strength: The presence of other ions in the solution can influence the activity of the ions involved in the acid-base equilibrium. This can affect the accuracy of calculations. Activity coefficients are sometimes used to adjust for this effect.
-
Temperature: The pKa of an acid is temperature-dependent. Calculations should account for temperature variations, especially when working with precise measurements.
-
Complexation: The presence of metal ions or other ligands that can form complexes with the acid or its conjugate base can significantly alter the equilibrium and affect the pH.
Practical Applications and Importance
The ability to calculate pH given pKa finds extensive application in various fields:
-
Biochemistry: pH plays a critical role in enzyme activity, protein folding, and many other biochemical processes. Understanding how pH changes affect biological systems is crucial.
-
Medicine: Maintaining the correct pH in body fluids is essential for health. Many pharmaceutical formulations utilize buffer systems to control pH.
-
Environmental Science: The pH of water bodies significantly influences the survival of aquatic organisms and overall water quality.
-
Chemical Engineering: Many industrial processes require precise pH control for optimal performance and product quality.
-
Agriculture: Soil pH is a key factor affecting nutrient availability and crop yield. Understanding how pH influences nutrient uptake and plant growth is paramount.
Conclusion
Calculating pH given pKa is a vital skill in chemistry and related fields. Mastering the Henderson-Hasselbalch equation and the approaches outlined in this guide will empower you to understand and predict the pH of different solutions, improving your understanding of acid-base chemistry and its applications. While the approximation method offers a convenient and often sufficient solution for weak acid calculations, the quadratic equation method provides a more accurate solution when needed. Remember to account for potential factors like ionic strength and temperature for more precise results in complex scenarios.
Latest Posts
Latest Posts
-
Is 3 4 More Than 1 2
Apr 02, 2025
-
5 Letter Words End With On
Apr 02, 2025
-
What Percent Is 3 Of 12
Apr 02, 2025
-
Volume Of A Cylinder In Cubic Feet
Apr 02, 2025
-
69 Is The Square Root Of
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about How To Find Ph Given Pka . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
