Is 3 4 More Than 1 2
Juapaving
Apr 02, 2025 · 5 min read
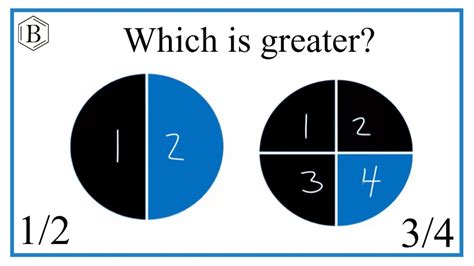
Table of Contents
Is 3/4 More Than 1/2? A Deep Dive into Fraction Comparison
Comparing fractions might seem like a simple task, especially when dealing with seemingly straightforward examples like 3/4 and 1/2. However, a solid understanding of fraction comparison is crucial for various aspects of mathematics and beyond. This comprehensive guide will not only answer the question "Is 3/4 more than 1/2?" but also delve into the underlying principles, providing you with the tools to compare any two fractions confidently.
Understanding Fractions: A Refresher
Before jumping into the comparison, let's ensure we have a firm grasp of what fractions represent. A fraction is a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered.
For example, in the fraction 3/4, the denominator (4) tells us the whole is divided into four equal parts. The numerator (3) indicates we're considering three of those four parts.
Methods for Comparing Fractions
Several methods can be used to compare fractions effectively. Let's explore the most common and reliable approaches:
1. Finding a Common Denominator
This is perhaps the most straightforward method. To compare two fractions, we convert them into equivalent fractions with the same denominator. This allows for a direct comparison of their numerators.
Let's compare 3/4 and 1/2 using this method:
-
Find the least common multiple (LCM) of the denominators: The denominators are 4 and 2. The LCM of 4 and 2 is 4.
-
Convert the fractions to equivalent fractions with the common denominator:
- 3/4 already has a denominator of 4.
- To convert 1/2 to an equivalent fraction with a denominator of 4, we multiply both the numerator and denominator by 2: (1 * 2) / (2 * 2) = 2/4
-
Compare the numerators: Now we compare 3/4 and 2/4. Since 3 > 2, we conclude that 3/4 > 1/2.
2. Using Decimal Equivalents
Another effective method involves converting the fractions to their decimal equivalents. This approach is particularly useful when dealing with fractions that are difficult to compare using a common denominator.
Let's compare 3/4 and 1/2 using decimal equivalents:
- Convert 3/4 to a decimal: 3 ÷ 4 = 0.75
- Convert 1/2 to a decimal: 1 ÷ 2 = 0.5
- Compare the decimals: Since 0.75 > 0.5, we conclude that 3/4 > 1/2.
3. Visual Representation
Visual aids, such as pie charts or fraction bars, can be extremely helpful, especially for beginners. Drawing a representation of each fraction allows for a clear visual comparison.
Imagine two identical circles. Divide one circle into four equal parts and shade three of them (representing 3/4). Divide the other circle into two equal parts and shade one of them (representing 1/2). By visually comparing the shaded areas, it's evident that 3/4 represents a larger portion than 1/2.
Why Understanding Fraction Comparison is Important
The ability to compare fractions is fundamental to many mathematical concepts and real-world applications. Here are some examples:
-
Solving Equations: Many algebraic equations involve fractions, and comparing them is crucial for finding solutions.
-
Data Analysis: Interpreting data represented as fractions (e.g., proportions, percentages) requires understanding how to compare them.
-
Measurement: Measuring quantities often involves fractions (e.g., inches, centimeters). Comparing fractional measurements is essential for accuracy.
-
Cooking and Baking: Recipes frequently use fractional measurements, and understanding fraction comparison ensures the correct proportions are used.
Beyond the Basics: Comparing More Complex Fractions
The methods discussed above apply to simple fractions. However, when dealing with more complex fractions (e.g., fractions with larger numbers or mixed numbers), the process might require more steps.
Comparing Fractions with Larger Numbers: The common denominator method remains the most reliable approach. Finding the LCM of larger numbers might require prime factorization or other techniques.
Comparing Mixed Numbers: A mixed number consists of a whole number and a fraction (e.g., 1 1/2). To compare mixed numbers, compare the whole numbers first. If the whole numbers are different, the larger whole number represents the larger mixed number. If the whole numbers are the same, compare the fractional parts using the methods discussed above.
Practical Applications: Real-World Examples
Let's look at some real-world scenarios where comparing fractions is essential:
-
Determining the Better Deal: Suppose you're choosing between two pizzas. One is 3/4 of the size of a standard pizza, while the other is only 1/2. Knowing that 3/4 > 1/2, you'll choose the larger pizza.
-
Managing Time: If a task requires 1/2 an hour and you only have 3/4 of an hour available, you'll know you have enough time.
-
Sharing Resources: If you need to divide 3/4 of a cake among four friends and 1/2 of a different cake among two friends, you can determine which share is larger.
Conclusion: Mastering Fraction Comparison
Understanding how to compare fractions is a fundamental skill with far-reaching applications. By mastering the techniques of finding common denominators, using decimal equivalents, and employing visual aids, you can confidently compare any two fractions. This skill is not only crucial for academic success but also for navigating everyday situations where fractional quantities are involved. Regular practice and a solid grasp of the underlying concepts will make comparing fractions a straightforward and efficient process. Remember, consistent practice is key to mastering any mathematical concept, and fraction comparison is no exception. The more you practice, the more comfortable and confident you will become in tackling even the most complex fraction comparisons. This empowers you to approach mathematical problems and real-world challenges with increased accuracy and efficiency.
Latest Posts
Latest Posts
-
How Many Bones Does Shark Have
Apr 03, 2025
-
Ca Oh 2 Acid Or Base
Apr 03, 2025
-
Quadrilateral With One Pair Of Parallel Sides
Apr 03, 2025
-
Any Change In Velocity Is Called
Apr 03, 2025
-
What Is The Difference Heat And Temperature
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Is 3 4 More Than 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
