What Percent Is 3 Of 12
Juapaving
Apr 02, 2025 · 5 min read
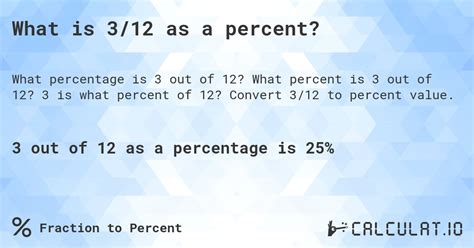
Table of Contents
What Percent is 3 of 12? A Deep Dive into Percentage Calculations
Percentages are fundamental to everyday life, from calculating sales tax and discounts to understanding statistics and financial reports. Knowing how to calculate percentages accurately is a crucial skill. This article will explore the question, "What percent is 3 of 12?" in detail, providing a comprehensive understanding of the process, its applications, and related concepts. We'll go beyond a simple answer, delving into the methodology, practical examples, and various methods for solving percentage problems.
Understanding Percentages: The Basics
A percentage is a fraction or ratio expressed as a number out of 100. The symbol used to represent percentages is "%". For instance, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
Calculating "What Percent is 3 of 12?"
The core question, "What percent is 3 of 12?", asks us to find what proportion of 12 is represented by the number 3, expressed as a percentage. Here's how we solve it:
Method 1: Using the Formula
The fundamental formula for calculating percentages is:
(Part / Whole) x 100% = Percentage
In our case:
- Part: 3
- Whole: 12
Substituting these values into the formula:
(3 / 12) x 100% = 0.25 x 100% = 25%
Therefore, 3 is 25% of 12.
Method 2: Simplifying the Fraction
We can simplify the fraction 3/12 before multiplying by 100%. Both the numerator (3) and the denominator (12) are divisible by 3:
3/12 simplifies to 1/4
Now, converting the fraction 1/4 to a percentage:
(1 / 4) x 100% = 0.25 x 100% = 25%
This method demonstrates that simplifying fractions can often make percentage calculations easier.
Method 3: Using Proportions
We can also solve this using proportions. We set up a proportion where x represents the percentage we want to find:
3/12 = x/100
Cross-multiplying:
12x = 300
Solving for x:
x = 300 / 12 = 25
Therefore, x = 25%, confirming our previous calculations.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is essential in numerous real-world situations. Here are some examples:
1. Sales and Discounts:
Imagine a store offering a 25% discount on an item originally priced at $48. To calculate the discount, we use the same percentage formula:
(25/100) x $48 = $12
The discount is $12, making the final price $48 - $12 = $36. This scenario directly relates to our original problem, as the discount percentage mirrors the percentage of 3 in 12.
2. Taxes and Interest:
Sales tax, income tax, and interest rates are all expressed as percentages. Understanding percentage calculations allows you to accurately compute the total cost of an item including tax or the amount of interest accrued on a loan or investment.
3. Statistics and Data Analysis:
Percentages are ubiquitous in statistics. They are used to represent proportions in data sets, enabling comparisons and analyses. For example, understanding that 25% of respondents preferred a particular product provides valuable market research insights.
4. Financial Planning:
Budgeting, investment analysis, and retirement planning all heavily rely on percentage calculations. Determining the percentage of income allocated to savings or the return on investment requires precise percentage computations.
5. Grade Calculation:
In educational settings, percentages are used to represent grades. If you score 3 out of 12 on a quiz, your grade is 25%, clearly illustrating the relevance of this calculation in academic contexts.
Expanding on Percentage Calculations: More Complex Scenarios
While our original problem was relatively straightforward, percentage calculations can become more complex. Let's explore some scenarios that build upon the basic principles:
Calculating the Whole Given the Percentage and Part
Suppose you know that 25% of a number is 15. How can you find the original number (the whole)? We can set up a proportion:
25/100 = 15/x
Cross-multiplying:
25x = 1500
x = 1500 / 25 = 60
Therefore, the original number is 60.
Calculating the Percentage Increase or Decrease
Percentage increase or decrease calculations are commonly used to show changes over time. For example, if a quantity increases from 10 to 15, the percentage increase is calculated as follows:
[(15 - 10) / 10] x 100% = 50%
Working with Multiple Percentages
Sometimes, you need to work with multiple percentages sequentially. For instance, you might have a 20% discount followed by a 10% sales tax. These calculations require careful step-by-step application of the percentage formula.
Tips and Tricks for Mastering Percentage Calculations
- Practice Regularly: Consistent practice is key to mastering percentage calculations. Solve various problems to build confidence and speed.
- Understand the Formula: Thoroughly grasp the fundamental percentage formula: (Part / Whole) x 100%.
- Simplify Fractions: Simplifying fractions before multiplying by 100% can often streamline the process.
- Use Proportions: Setting up proportions can be a helpful alternative method, especially for more complex problems.
- Use Calculators: Calculators can assist with more complex calculations, but understanding the underlying principles remains crucial.
Conclusion: The Power of Percentage Calculations
The seemingly simple question, "What percent is 3 of 12?", opens the door to a vast world of percentage calculations. From everyday transactions to complex financial models, understanding percentages is essential for navigating the numerical landscape of modern life. By mastering the basic principles, techniques, and applications discussed in this article, you'll be well-equipped to confidently tackle various percentage-related challenges. Remember, consistent practice and a thorough understanding of the underlying concepts are the keys to mastering this fundamental mathematical skill.
Latest Posts
Latest Posts
-
How Many Bones Does Shark Have
Apr 03, 2025
-
Ca Oh 2 Acid Or Base
Apr 03, 2025
-
Quadrilateral With One Pair Of Parallel Sides
Apr 03, 2025
-
Any Change In Velocity Is Called
Apr 03, 2025
-
What Is The Difference Heat And Temperature
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 3 Of 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
