How To Determine The Order Of The Matrix
Juapaving
Mar 30, 2025 · 5 min read
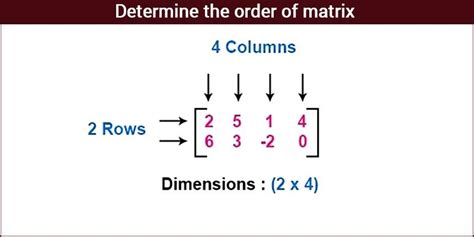
Table of Contents
How to Determine the Order of a Matrix: A Comprehensive Guide
Determining the order of a matrix is a fundamental concept in linear algebra. Understanding matrix order is crucial for performing various matrix operations, solving linear equations, and comprehending the structure of data represented in matrix form. This comprehensive guide will delve into the definition of matrix order, explain how to determine it, and illustrate the concept with numerous examples. We'll also explore how the order of a matrix impacts different operations and applications.
What is the Order of a Matrix?
A matrix is a rectangular array of numbers, symbols, or expressions, arranged in rows and columns. The order (or dimension) of a matrix is defined by the number of rows and columns it possesses. It's expressed as m x n, where:
- m represents the number of rows.
- n represents the number of columns.
A matrix with m rows and n columns is referred to as an m x n matrix, or an "m by n" matrix.
How to Determine the Matrix Order: A Step-by-Step Guide
Determining the order of a matrix is straightforward. Follow these steps:
-
Count the number of rows: Rows are horizontal lines of elements in the matrix. Carefully count each row.
-
Count the number of columns: Columns are vertical lines of elements. Count each column meticulously.
-
Express the order: Write the order as m x n, where m is the number of rows and n is the number of columns.
Let's illustrate this with examples:
Example 1:
Consider the matrix:
A = [ 1 2 3 ]
[ 4 5 6 ]
- Number of rows (m) = 2
- Number of columns (n) = 3
Therefore, the order of matrix A is 2 x 3.
Example 2:
Consider the matrix:
B = [ 1 4 ]
[ 2 5 ]
[ 3 6 ]
- Number of rows (m) = 3
- Number of columns (n) = 2
Therefore, the order of matrix B is 3 x 2.
Example 3:
Consider the matrix:
C = [ 10 ]
- Number of rows (m) = 1
- Number of columns (n) = 1
Therefore, the order of matrix C is 1 x 1. This is also known as a scalar matrix.
Example 4:
Consider the matrix:
D = [ 1 2 3 4 5 ]
- Number of rows (m) = 1
- Number of columns (n) = 5
Therefore, the order of matrix D is 1 x 5. This is a row matrix or row vector.
Example 5:
Consider the matrix:
E = [ 1 ]
[ 2 ]
[ 3 ]
[ 4 ]
[ 5 ]
- Number of rows (m) = 5
- Number of columns (n) = 1
Therefore, the order of matrix E is 5 x 1. This is a column matrix or column vector.
Special Types of Matrices Based on Order
The order of a matrix plays a crucial role in classifying it into different types:
-
Square Matrix: A square matrix has an equal number of rows and columns (m = n). Examples include 2 x 2, 3 x 3, and 4 x 4 matrices. Many special properties and operations apply only to square matrices (e.g., determinants, inverses).
-
Rectangular Matrix: A rectangular matrix has an unequal number of rows and columns (m ≠ n). The examples above (except for the 1x1 and the row and column vectors) are all rectangular matrices.
-
Row Matrix (Row Vector): A row matrix has only one row (m = 1).
-
Column Matrix (Column Vector): A column matrix has only one column (n = 1).
-
Null Matrix (Zero Matrix): A null matrix is a matrix where all elements are zero. The order of a null matrix can be any m x n.
-
Diagonal Matrix: A square matrix where all elements are zero except for those on the main diagonal (from the top-left to bottom-right).
-
Identity Matrix: A special type of diagonal matrix where all elements on the main diagonal are 1. Identity matrices are crucial in many matrix operations.
Importance of Matrix Order in Matrix Operations
The order of matrices is critical when performing operations like addition, subtraction, and multiplication. Let's look at how order affects these operations:
Matrix Addition and Subtraction
Matrices can be added or subtracted only if they have the same order (the same number of rows and columns). If the matrices have different orders, these operations are undefined.
Matrix Multiplication
Matrix multiplication is more complex. For two matrices A (of order m x n) and B (of order p x q), multiplication (A x B) is only defined if the number of columns in A is equal to the number of rows in B (n = p). The resulting matrix (AB) will have the order m x q.
Applications of Matrix Order
Understanding matrix order is vital across diverse fields, including:
-
Computer Graphics: Matrices are used extensively to represent transformations (rotation, scaling, translation) of objects in 3D space. The order of these matrices determines how transformations are applied.
-
Machine Learning: Matrices are fundamental data structures in machine learning algorithms. The dimensions of matrices (their order) directly affect the complexity and efficiency of algorithms like linear regression, support vector machines, and neural networks.
-
Image Processing: Images are often represented as matrices, where each element corresponds to a pixel's color value. Matrix operations are used for image enhancement, compression, and manipulation. The matrix order dictates the resolution and size of the image.
-
Physics and Engineering: Matrices are utilized to solve systems of linear equations in various engineering disciplines like structural analysis, circuit analysis, and fluid dynamics. The order of matrices corresponds to the number of variables and equations in these systems.
-
Economics and Finance: Matrix algebra is used in econometrics and financial modeling to represent economic relationships and portfolios. The order of matrices involved in these models reflects the complexity of the system being analyzed.
Conclusion
Determining the order of a matrix is a fundamental skill in linear algebra and is essential for understanding matrix operations and applications. Knowing the number of rows and columns allows for the correct application of various mathematical processes and the interpretation of data structures across numerous fields. This understanding is crucial for anyone working with matrices in any quantitative field. By mastering this simple yet powerful concept, you unlock the door to a deeper comprehension of linear algebra and its extensive real-world applications.
Latest Posts
Latest Posts
-
Differences Between Primary Data And Secondary Data
Apr 01, 2025
-
Where Glucose Gets Broken Into Pyruvate In The Cell
Apr 01, 2025
-
Find The Inverse Of The Relation
Apr 01, 2025
-
How Are Cellular Respiration And Photosynthesis Related
Apr 01, 2025
-
How Many Rna Polymerases Are Found In Prokaryotes
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about How To Determine The Order Of The Matrix . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
