How Many Degrees In An Equilateral Triangle
Juapaving
Mar 30, 2025 · 5 min read
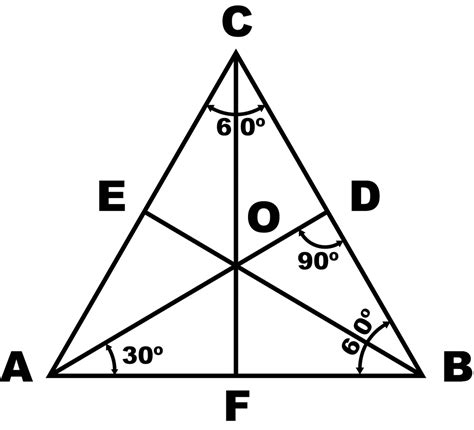
Table of Contents
How Many Degrees in an Equilateral Triangle? A Comprehensive Guide
The question, "How many degrees in an equilateral triangle?" might seem simple at first glance. However, understanding the answer fully delves into fundamental concepts of geometry, providing a springboard for exploring more complex geometric relationships. This comprehensive guide will not only answer the question definitively but also explore the properties of equilateral triangles, their applications, and related geometric theorems.
Understanding Triangles: A Foundation in Geometry
Before diving into the specifics of equilateral triangles, let's establish a basic understanding of triangles in general. A triangle, in its simplest definition, is a two-dimensional polygon composed of three straight sides and three angles. The sum of the interior angles of any triangle, regardless of its type (equilateral, isosceles, scalene), always equals 180 degrees. This is a cornerstone of Euclidean geometry and is crucial for solving countless geometric problems.
Types of Triangles: A Quick Overview
Triangles are classified based on the lengths of their sides and the measures of their angles. The three main types are:
- Equilateral Triangles: All three sides are equal in length, and all three angles are equal (60 degrees each).
- Isosceles Triangles: Two sides are equal in length, and the angles opposite those sides are also equal.
- Scalene Triangles: All three sides have different lengths, and all three angles have different measures.
Understanding these classifications is fundamental to grasping the unique properties of each triangle type, particularly the equilateral triangle, which is the focus of this article.
The Equilateral Triangle: A Perfect Polygon
An equilateral triangle possesses a unique symmetry and elegance. Its defining characteristic is the equality of all three sides and angles. This perfect symmetry leads to several important properties:
Properties of an Equilateral Triangle:
- Equal Sides: All three sides are congruent (equal in length).
- Equal Angles: All three angles are congruent and measure 60 degrees each. This is a direct consequence of the equal side lengths.
- Centroid, Circumcenter, Incenter, and Orthocenter Coincidence: In an equilateral triangle, the centroid (intersection of medians), circumcenter (intersection of perpendicular bisectors), incenter (intersection of angle bisectors), and orthocenter (intersection of altitudes) all coincide at a single point. This is a unique property not shared by other triangle types.
- Rotational Symmetry: An equilateral triangle exhibits rotational symmetry of order 3. This means it can be rotated by 120 degrees about its center and still appear unchanged.
- Reflectional Symmetry: It possesses three lines of reflectional symmetry, each passing through a vertex and the midpoint of the opposite side.
Proof: Why 180 Degrees in a Triangle?
The fact that the sum of the interior angles of any triangle equals 180 degrees is not merely an assertion; it's a provable theorem. Several approaches can demonstrate this, but here's one common method:
- Draw a Triangle: Start with any triangle ABC.
- Draw a Parallel Line: Draw a line through point C parallel to side AB.
- Identify Alternate Interior Angles: Notice that the angles formed by the intersection of this parallel line and lines AC and BC are alternate interior angles. Alternate interior angles are equal when a transversal line intersects two parallel lines. Therefore, angle 1 is equal to angle A, and angle 2 is equal to angle B.
- Sum of Angles on a Straight Line: Observe that angles 1, 2, and C lie on a straight line. The sum of angles on a straight line is always 180 degrees.
- Conclusion: Since angle 1 = angle A and angle 2 = angle B, we can conclude that angle A + angle B + angle C = 180 degrees.
This proof holds true for any triangle, regardless of its shape or size.
How Many Degrees in an Equilateral Triangle? The Definitive Answer
Given the fundamental rule that the sum of angles in any triangle is 180 degrees, and considering that an equilateral triangle has three equal angles, we can easily calculate the measure of each angle:
180 degrees / 3 angles = 60 degrees/angle
Therefore, each angle in an equilateral triangle measures 60 degrees.
Applications of Equilateral Triangles
Equilateral triangles are not merely abstract geometric concepts; they find practical applications in various fields:
- Architecture and Engineering: Their inherent stability and symmetry make them valuable in structural design, appearing in building frameworks, trusses, and other constructions.
- Art and Design: The pleasing aesthetic symmetry of equilateral triangles is often utilized in art, design, and logos.
- Nature: Equilateral triangles, while not as prevalent as other shapes in nature, can sometimes be observed in crystal structures and other natural formations.
- Tessellations: Equilateral triangles can perfectly tessellate (tile) a plane, meaning they can cover a surface without gaps or overlaps, forming regular hexagonal patterns. This property is found in honeycombs and some other natural structures.
- Mathematics and Computer Science: They serve as fundamental building blocks in various mathematical proofs and algorithms, particularly in computational geometry.
Related Geometric Theorems and Concepts
The understanding of equilateral triangles is intertwined with several important geometric theorems and concepts:
- Pythagorean Theorem: While not directly applicable to finding angles in an equilateral triangle (since it deals with side lengths in right-angled triangles), the Pythagorean theorem is a crucial component in many related geometric calculations.
- Trigonometry: Trigonometric functions (sine, cosine, tangent) can be used to calculate side lengths and angles in equilateral triangles, providing alternative methods for solving problems.
- Similar Triangles: The concept of similar triangles (triangles with the same angles but different side lengths) is relevant when dealing with scaled versions of equilateral triangles.
- Area Calculation: The area of an equilateral triangle can be calculated using formulas involving its side length, further highlighting the relationship between angles and sides.
Conclusion: More Than Just 60 Degrees
While the answer to "How many degrees in an equilateral triangle?" is a simple "60 degrees per angle," understanding the underlying principles and exploring the various properties and applications of equilateral triangles reveals a deeper appreciation for the elegance and utility of this fundamental geometric shape. Its perfect symmetry and unique characteristics make it a cornerstone in many areas of mathematics, science, engineering, and design. This comprehensive exploration has hopefully provided a thorough understanding of this seemingly simple yet profoundly important geometric figure.
Latest Posts
Latest Posts
-
The Movement Of Water Across A Semipermeable Membrane Is Called
Apr 01, 2025
-
Differences Between Primary Data And Secondary Data
Apr 01, 2025
-
Where Glucose Gets Broken Into Pyruvate In The Cell
Apr 01, 2025
-
Find The Inverse Of The Relation
Apr 01, 2025
-
How Are Cellular Respiration And Photosynthesis Related
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about How Many Degrees In An Equilateral Triangle . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
