What Is 4 The Square Root Of
Juapaving
Mar 31, 2025 · 4 min read
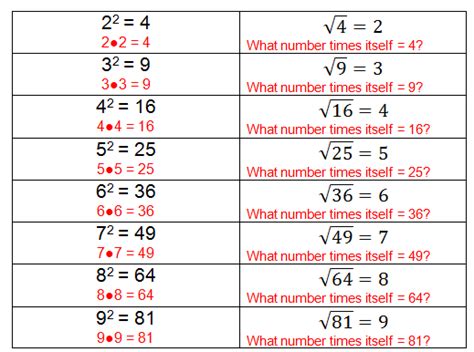
Table of Contents
Decoding the Mystery: What is the Square Root of 4? And Beyond...
The seemingly simple question, "What is the square root of 4?" often serves as a gateway to understanding a broader mathematical concept. While the answer itself is straightforward (2), delving deeper reveals fascinating connections to algebra, geometry, and even advanced mathematical fields. This article aims to explore not just the answer, but the why behind it, expanding on the concept of square roots and their applications.
Understanding Square Roots: A Foundational Concept
At its core, a square root is a number that, when multiplied by itself, produces a given number. Think of it as the reverse operation of squaring a number. Squaring a number means multiplying it by itself (e.g., 3² = 3 × 3 = 9). The square root, denoted by the symbol √, asks the question: "What number, when multiplied by itself, equals this number?"
In the case of 4, the square root is 2 because 2 × 2 = 4. Therefore, √4 = 2. It's important to note that, for positive numbers, there are two square roots: a positive and a negative one. While √4 = 2, it's also true that (-2) × (-2) = 4. However, the principal square root (the one typically denoted by the √ symbol) is the positive square root.
Beyond 4: Exploring Other Square Roots
Let's expand our understanding by examining other square roots:
- √9 = 3 (because 3 × 3 = 9)
- √16 = 4 (because 4 × 4 = 16)
- √25 = 5 (because 5 × 5 = 25)
- √0 = 0 (because 0 × 0 = 0)
Notice a pattern? Perfect squares (numbers that are the squares of integers) have whole number square roots. But what about numbers that aren't perfect squares?
Dealing with Non-Perfect Squares: Irrational Numbers
Numbers like √2, √3, √5, etc., are not perfect squares. Their square roots are irrational numbers. Irrational numbers cannot be expressed as a simple fraction; their decimal representation goes on forever without repeating. While we can approximate these values using calculators or computers, they cannot be represented precisely as a finite decimal.
For example, √2 ≈ 1.41421356..., a number that continues infinitely without repeating. This illustrates that the concept of square roots extends beyond simple, whole number solutions.
Geometric Interpretation: The Square
The name "square root" itself hints at its geometrical significance. Consider a square with an area of 4 square units. The length of each side of this square is the square root of 4, which is 2 units. This visual representation solidifies the concept: the square root is the length of the side of a square with the given area. This relationship extends to other numbers; the square root of any area represents the side length of a square with that area.
Square Roots in Equations: Solving for Unknowns
Square roots play a vital role in solving algebraic equations. Consider the equation x² = 25. To find the value of x, we take the square root of both sides: √x² = √25, which simplifies to x = ±5. This highlights the importance of considering both positive and negative solutions when dealing with equations involving squares.
The application extends to more complex equations. For instance, in physics, calculating the velocity of an object often involves the use of square roots.
Advanced Applications: Calculus and Beyond
The concept of square roots extends far beyond basic arithmetic and algebra. In calculus, the derivative and integral of functions often involve square roots. They also appear in various formulas within physics, engineering, and computer science.
For example, the Pythagorean theorem (a² + b² = c²), fundamental to geometry and trigonometry, requires the use of square roots to solve for the length of a hypotenuse given the lengths of two legs.
Approximating Square Roots: Techniques and Methods
Before the widespread availability of calculators, mathematicians developed various methods for approximating square roots. One common method is the Babylonian method (also known as Heron's method), an iterative algorithm that refines an initial guess to obtain a progressively more accurate approximation.
While calculators provide instant answers, understanding the underlying principles and alternative methods offers valuable insight into the nature of square roots and numerical computation.
Square Roots of Negative Numbers: Introducing Imaginary Numbers
The square root of a negative number, such as √-1, leads to the concept of imaginary numbers. This expands the number system beyond real numbers and opens up a whole new realm of mathematics dealing with complex numbers (numbers with both real and imaginary parts). Imaginary numbers are crucial in many areas of advanced mathematics, physics (especially quantum mechanics), and electrical engineering.
The imaginary unit, denoted by i, is defined as √-1, allowing for the calculation of square roots for any negative number. For instance, √-4 = 2i.
Conclusion: The Square Root of 4 and its Profound Implications
The seemingly simple question, "What is the square root of 4?" serves as a springboard into a vast and multifaceted mathematical landscape. From basic arithmetic to advanced calculus, the concept of square roots permeates various branches of mathematics and its applications in science and engineering. Understanding its implications, including the existence of both rational and irrational numbers, and the extension to complex numbers, provides a deeper appreciation for the richness and complexity of mathematics. The seemingly simple answer, 2, unlocks a universe of mathematical exploration. The journey from a simple question to a profound understanding showcases the elegance and power of mathematical concepts.
Latest Posts
Latest Posts
-
Common Multiples Of 18 And 24
Apr 01, 2025
-
What Are The Factors Of 94
Apr 01, 2025
-
Can You Have A Negative Acceleration
Apr 01, 2025
-
What Is The Square Root 69
Apr 01, 2025
-
Difference Between Communicable And Non Communicable Disease
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about What Is 4 The Square Root Of . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
