How Many Factors Does A Composite Number Have
Juapaving
Mar 31, 2025 · 5 min read
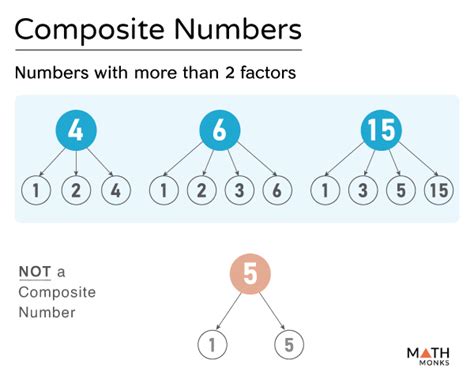
Table of Contents
How Many Factors Does a Composite Number Have? Unlocking the Secrets of Factorization
Determining the number of factors a composite number possesses is a fundamental concept in number theory with wide-ranging applications in mathematics, computer science, and cryptography. While seemingly simple, understanding the process reveals a fascinating interplay between prime factorization and combinatorial principles. This comprehensive guide delves deep into the mechanics of factor counting, equipping you with the knowledge to efficiently determine the number of factors for any composite number.
Understanding Factors and Composite Numbers
Before embarking on the intricacies of factor counting, let's solidify our understanding of the core concepts:
Factors (Divisors): Factors of a number are whole numbers that divide the number exactly, leaving no remainder. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12.
Composite Numbers: A composite number is a positive integer greater than 1 that is not a prime number. A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. Composite numbers can be expressed as the product of prime numbers. For example, 12 is a composite number because it's divisible by 2 and 3 (12 = 2 x 2 x 3).
The Prime Factorization Method: The Cornerstone of Factor Counting
The key to efficiently determining the number of factors of a composite number lies in its prime factorization. This process involves expressing the composite number as a product of its prime factors. For instance, the prime factorization of 12 is 2² x 3¹.
Why Prime Factorization is Crucial: Each factor of the composite number is a combination of these prime factors raised to powers less than or equal to their exponents in the prime factorization. This fundamental connection unlocks the pathway to calculating the total number of factors.
Calculating the Number of Factors: The Formula
Once we have the prime factorization of a composite number, we can utilize a straightforward formula to calculate its total number of factors. Let's assume the prime factorization of a composite number n is given by:
n = p₁<sup>a₁</sup> x p₂<sup>a₂</sup> x p₃<sup>a₃</sup> ... x p<sub>k</sub><sup>a<sub>k</sub></sup>
where p₁, p₂, p₃,... p<sub>k</sub> are distinct prime numbers and a₁, a₂, a₃,... a<sub>k</sub> are their respective exponents.
The total number of factors (τ(n) or d(n)) of n is calculated using the following formula:
τ(n) = (a₁ + 1)(a₂ + 1)(a₃ + 1)...(a<sub>k</sub> + 1)
Let's illustrate this with examples:
Example 1: Finding the number of factors of 12
- Prime Factorization: 12 = 2² x 3¹
- Applying the formula: τ(12) = (2 + 1)(1 + 1) = 3 x 2 = 6
- Therefore, 12 has 6 factors: 1, 2, 3, 4, 6, and 12.
Example 2: Finding the number of factors of 360
- Prime Factorization: 360 = 2³ x 3² x 5¹
- Applying the formula: τ(360) = (3 + 1)(2 + 1)(1 + 1) = 4 x 3 x 2 = 24
- Therefore, 360 has 24 factors.
Example 3: A larger number - 2520
- Prime Factorization: 2520 = 2³ x 3² x 5¹ x 7¹
- Applying the formula: τ(2520) = (3+1)(2+1)(1+1)(1+1) = 4 x 3 x 2 x 2 = 48
- Therefore, 2520 has 48 factors.
Why Does This Formula Work?
The formula's effectiveness stems from the fundamental principle of combinatorics. Each factor of the composite number is formed by selecting a combination of the prime factors raised to powers less than or equal to their exponents in the prime factorization.
Consider the prime factorization p₁<sup>a₁</sup> x p₂<sup>a₂</sup>. To construct a factor, we can choose any power of p₁ from 0 to a₁, which gives us (a₁ + 1) options. Similarly, we have (a₂ + 1) options for choosing the power of p₂. By the multiplication principle of combinatorics, the total number of ways to form a factor is the product of these options: (a₁ + 1)(a₂ + 1). This extends seamlessly to any number of distinct prime factors.
Advanced Applications and Extensions
The concept of factor counting extends far beyond basic arithmetic. It finds practical applications in:
-
Cryptography: Understanding the number of factors is crucial in analyzing the security of certain encryption algorithms. The difficulty of factoring large numbers into their prime components underpins the strength of some cryptographic systems.
-
Computer Science: Algorithms for prime factorization and factor counting are essential in various computational tasks, particularly in optimization problems and database management.
-
Number Theory: The function τ(n), which counts the number of divisors, is a vital object of study in number theory, with deep connections to other number-theoretic functions and concepts like the divisor sum function.
-
Combinatorics: The formula for the number of factors provides a beautiful example of the power of combinatorial reasoning in solving number-theoretic problems.
Handling Special Cases
While the formula generally works effectively, it’s important to consider some specific scenarios:
-
Prime Numbers: A prime number only has two factors: 1 and itself. The formula still applies; since its prime factorization has only one prime factor with an exponent of 1, the number of factors is 1+1=2.
-
Number 1: The number 1 is neither prime nor composite, and it has only one factor: 1. This is a special case that falls outside the typical composite number analysis.
Practical Tips and Exercises
To solidify your understanding, practice finding the prime factorizations and then the number of factors for various composite numbers. Start with smaller numbers and gradually increase the complexity.
Exercise 1: Find the number of factors for 72.
Exercise 2: Determine the number of factors for 1000.
Exercise 3: Calculate the number of factors for 2025.
By mastering the techniques outlined in this guide, you'll develop a comprehensive understanding of factor counting and its broad applications within the fascinating world of number theory and beyond. Remember, the key lies in understanding prime factorization and applying the formula effectively to unlock the secrets of a composite number's divisors. Happy factoring!
Latest Posts
Latest Posts
-
Solid Has Definite Shape And Volume
Apr 01, 2025
-
What Animal Lays Eggs Thats Not A Bird
Apr 01, 2025
-
Common Multiples Of 18 And 24
Apr 01, 2025
-
What Are The Factors Of 94
Apr 01, 2025
-
Can You Have A Negative Acceleration
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about How Many Factors Does A Composite Number Have . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
