What Is A Perfect Cube In Mathematics
Juapaving
Mar 31, 2025 · 5 min read
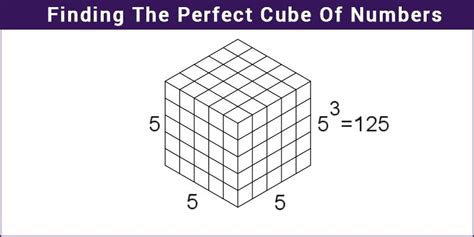
Table of Contents
What is a Perfect Cube in Mathematics? A Comprehensive Guide
Perfect cubes, a fundamental concept in mathematics, hold significant importance in various areas, from basic arithmetic to advanced algebraic manipulations. Understanding perfect cubes is crucial for simplifying expressions, solving equations, and grasping more complex mathematical concepts. This comprehensive guide delves deep into the world of perfect cubes, exploring their definition, properties, identification, applications, and relationship with other mathematical concepts.
Defining a Perfect Cube
A perfect cube, in its simplest form, is a number obtained by multiplying an integer by itself three times. In mathematical notation, a perfect cube is represented as n³, where 'n' is any integer. This means we're cubing the integer 'n,' or raising it to the power of 3. For example:
- 1³ = 1 × 1 × 1 = 1
- 2³ = 2 × 2 × 2 = 8
- 3³ = 3 × 3 × 3 = 27
- 4³ = 4 × 4 × 4 = 64
- 5³ = 5 × 5 × 5 = 125
And so on. These numbers – 1, 8, 27, 64, 125, etc. – are all perfect cubes because they are the result of cubing an integer. Note that negative integers also yield perfect cubes. For instance, (-2)³ = -8. This is because a negative number cubed results in a negative number.
Properties of Perfect Cubes
Perfect cubes possess several unique properties that help in their identification and manipulation:
1. The Units Digit Pattern:
Observing the units digit of perfect cubes reveals a cyclical pattern. The units digit of a perfect cube can only be one of these digits: 0, 1, 8, 7, 4, 5, 6, 3, 2, 9. This pattern repeats. This property is useful for quickly eliminating numbers that cannot be perfect cubes. For example, a number ending in 7 could be a perfect cube (like 343 = 7³), but a number ending in 2 could also be a perfect cube.
2. Even and Odd Cubes:
A perfect cube will always be even if the base integer ('n') is even, and odd if the base integer is odd. This is directly related to the properties of even and odd numbers under multiplication.
3. Divisibility Rules:
Certain divisibility rules apply to perfect cubes. For instance, if a number is divisible by 8, it could potentially be a perfect cube. However, divisibility alone doesn't confirm a number as a perfect cube.
4. Sum of Cubes:
The sum of cubes has a well-known factorization: a³ + b³ = (a + b)(a² - ab + b²). This identity is invaluable for factoring and simplifying algebraic expressions.
5. Difference of Cubes:
Similarly, the difference of cubes also has a notable factorization: a³ - b³ = (a - b)(a² + ab + b²). This is another vital tool in algebraic manipulation.
Identifying Perfect Cubes
Identifying whether a given number is a perfect cube can be approached in several ways:
1. Prime Factorization:
The most reliable method involves prime factorization. Express the number as a product of its prime factors. If each prime factor has an exponent that is a multiple of 3, the number is a perfect cube. For example, let's check if 216 is a perfect cube:
216 = 2 × 108 = 2 × 2 × 54 = 2 × 2 × 2 × 27 = 2 × 2 × 2 × 3 × 9 = 2 × 2 × 2 × 3 × 3 × 3 = 2³ × 3³ = (2 × 3)³ = 6³
Since each prime factor (2 and 3) has an exponent that's a multiple of 3, 216 is a perfect cube.
2. Estimation and Cube Root:
For smaller numbers, estimation and calculating the cube root can be efficient. You can use a calculator or estimation techniques to find the cube root. If the cube root is an integer, the number is a perfect cube.
3. Using the Units Digit Pattern:
While not conclusive on its own, the units digit pattern can help eliminate possibilities quickly. If a number's units digit doesn't match the pattern of perfect cubes, it can't be a perfect cube.
Applications of Perfect Cubes
Perfect cubes find applications in various mathematical domains:
1. Algebra:
Perfect cubes are essential in algebraic manipulations, especially when simplifying expressions involving factoring, expanding, and solving equations. The sum and difference of cubes formulas are frequently used.
2. Geometry:
Perfect cubes are directly related to the volume of cubes. If the side length of a cube is an integer 'n', its volume will be n³.
3. Number Theory:
Perfect cubes play a role in number theory problems involving divisibility, factorization, and congruences.
4. Calculus:
The concept of perfect cubes extends to the study of derivatives and integrals in calculus.
Perfect Cubes and Other Mathematical Concepts
Perfect cubes are closely intertwined with several other mathematical concepts:
1. Cube Roots:
The cube root of a number is the number that, when cubed, gives the original number. The cube root of a perfect cube is always an integer. For example, the cube root of 64 is 4 (because 4³ = 64).
2. Polynomials:
Perfect cubes appear frequently in polynomial expressions, particularly when factoring or expanding cubic polynomials.
3. Geometry:
As mentioned earlier, perfect cubes represent the volume of cubes with integer side lengths. This connection extends to other three-dimensional geometric shapes.
Advanced Topics Related to Perfect Cubes
For those seeking a deeper understanding, here are some advanced concepts:
1. Sum of Consecutive Cubes:
The sum of consecutive cubes from 1 to n can be expressed as a perfect square: 1³ + 2³ + 3³ + ... + n³ = (n(n+1)/2)².
2. Higher-Dimensional Cubes:
The concept of cubes can be generalized to higher dimensions (hypercubes), but the underlying principle remains the same: a number raised to the power of the dimension.
3. Perfect Cubes in Number Theory Research:
Perfect cubes are frequently subjects of research within number theory, specifically in relation to Diophantine equations and other advanced number theoretic concepts.
Conclusion
Understanding perfect cubes is fundamental to success in various mathematical endeavors. From the simplicity of calculating the volume of a cube to the complexity of solving advanced algebraic equations, the concept of perfect cubes acts as a cornerstone. By grasping its definition, properties, and applications, one develops a deeper appreciation for the interconnectedness of various mathematical branches. This comprehensive guide aims to provide a solid foundation for further exploration of this intriguing area of mathematics. Remember to utilize the properties discussed here to efficiently identify and manipulate perfect cubes in your mathematical pursuits. Through practice and application, you'll become increasingly proficient in handling these essential components of the mathematical landscape.
Latest Posts
Latest Posts
-
No Name This Compound According To Iupac Nomenclature Rules Responses
Apr 01, 2025
-
Why Does Heat Not Transfer Through Solids By Convection
Apr 01, 2025
-
Solid Has Definite Shape And Volume
Apr 01, 2025
-
What Animal Lays Eggs Thats Not A Bird
Apr 01, 2025
-
Common Multiples Of 18 And 24
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about What Is A Perfect Cube In Mathematics . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
