How Do You Find The Base Area
Juapaving
Apr 02, 2025 · 6 min read
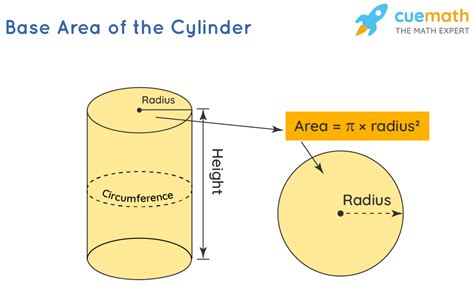
Table of Contents
How Do You Find the Base Area? A Comprehensive Guide
Finding the base area might seem straightforward, but the method varies significantly depending on the shape. This comprehensive guide will walk you through calculating the base area for various two-dimensional shapes and how those calculations translate into finding the base area of related three-dimensional objects. We'll cover everything from simple squares and rectangles to more complex polygons and irregular shapes. Mastering this skill is fundamental in various fields, from architecture and engineering to everyday tasks like calculating paint needs or carpet area.
Understanding "Base Area"
Before diving into calculations, let's clarify what we mean by "base area." The base area refers to the area of the base of a three-dimensional object. Think of it as the area of the flat surface upon which the object rests. This concept is crucial for calculating volume and surface area. However, the base itself isn't always the bottom face; in some cases, we might choose a specific face to be the base for calculation purposes.
Base Area of Common Two-Dimensional Shapes
The base area of a three-dimensional object directly depends on the shape of its base. Let's start by reviewing how to find the area of common two-dimensional shapes:
1. Square
A square is a simple polygon with four equal sides and four right angles.
Formula: Area = side * side = side²
Example: If a square has a side length of 5 cm, its area is 5 cm * 5 cm = 25 cm².
2. Rectangle
A rectangle is a quadrilateral with four right angles. Opposite sides are equal in length.
Formula: Area = length * width
Example: A rectangle with a length of 8 cm and a width of 3 cm has an area of 8 cm * 3 cm = 24 cm².
3. Triangle
A triangle is a polygon with three sides and three angles.
Formula: Area = (1/2) * base * height
Finding the height: The height is the perpendicular distance from the base to the opposite vertex. This is crucial; it's not necessarily a side of the triangle.
Example: A triangle with a base of 6 cm and a height of 4 cm has an area of (1/2) * 6 cm * 4 cm = 12 cm².
4. Circle
A circle is a set of points equidistant from a central point.
Formula: Area = π * radius²
Where π (pi) is approximately 3.14159.
Example: A circle with a radius of 7 cm has an area of π * (7 cm)² ≈ 153.94 cm².
5. Parallelogram
A parallelogram is a quadrilateral with opposite sides parallel and equal in length.
Formula: Area = base * height
Similar to triangles, the height is the perpendicular distance between the base and the opposite side.
Example: A parallelogram with a base of 10 cm and a height of 5 cm has an area of 10 cm * 5 cm = 50 cm².
6. Trapezoid
A trapezoid is a quadrilateral with at least one pair of parallel sides.
Formula: Area = (1/2) * (base1 + base2) * height
Where base1 and base2 are the lengths of the parallel sides, and the height is the perpendicular distance between them.
Example: A trapezoid with parallel sides of 8 cm and 12 cm and a height of 6 cm has an area of (1/2) * (8 cm + 12 cm) * 6 cm = 60 cm².
Base Area of Three-Dimensional Objects
Now, let's apply this knowledge to finding the base area of various three-dimensional shapes:
1. Cube
A cube is a three-dimensional shape with six square faces.
Finding the base area: Since the base is a square, simply use the square area formula: Area = side²
Example: A cube with a side of 4 cm has a base area of 4 cm * 4 cm = 16 cm².
2. Rectangular Prism (Cuboid)
A rectangular prism has six rectangular faces.
Finding the base area: The base is a rectangle, so use the rectangular area formula: Area = length * width
Example: A rectangular prism with a length of 10 cm, a width of 5 cm, and a height of 3 cm has a base area of 10 cm * 5 cm = 50 cm².
3. Cylinder
A cylinder is a three-dimensional shape with two circular bases and a curved surface connecting them.
Finding the base area: The base is a circle, so use the circle area formula: Area = π * radius²
Example: A cylinder with a radius of 6 cm has a base area of π * (6 cm)² ≈ 113.1 cm².
4. Triangular Prism
A triangular prism has two triangular bases and three rectangular faces.
Finding the base area: Find the area of the triangular base using the triangle area formula: Area = (1/2) * base * height
Example: A triangular prism with a triangular base having a base of 8 cm and a height of 5 cm has a base area of (1/2) * 8 cm * 5 cm = 20 cm².
5. Pyramid
A pyramid has a polygonal base and triangular faces meeting at a single point (the apex).
Finding the base area: The method depends on the shape of the base (square, rectangle, triangle, etc.). Use the appropriate formula for that shape.
Example: A square pyramid with a square base of side length 7 cm has a base area of 7 cm * 7 cm = 49 cm².
6. Cone
A cone is a three-dimensional shape with a circular base and a curved surface tapering to a point (the apex).
Finding the base area: The base is a circle, so use the circle area formula: Area = π * radius²
Example: A cone with a radius of 4 cm has a base area of π * (4 cm)² ≈ 50.27 cm².
Dealing with Irregular Shapes
For irregular shapes, finding the base area can be more challenging. Here are some approaches:
-
Divide and conquer: Break the irregular shape into smaller, regular shapes (rectangles, triangles, etc.). Calculate the area of each smaller shape and sum them up.
-
Grid method: Overlay a grid on the irregular shape and count the number of squares (or parts of squares) it covers. Estimate the area based on the grid's unit area.
-
Coordinate geometry: If you have the coordinates of the vertices of the irregular polygon, you can use the shoelace formula to calculate the area.
Practical Applications
Understanding how to find the base area has wide-ranging practical applications:
-
Construction and architecture: Calculating the foundation area, floor area, or roof area.
-
Engineering: Determining the cross-sectional area of beams, columns, or pipes.
-
Manufacturing: Calculating the surface area of products for painting, coating, or packaging.
-
Real estate: Measuring the area of land plots or building interiors.
-
Gardening: Calculating the area of a garden bed for planting.
Conclusion
Finding the base area is a crucial skill with numerous practical applications. While the basic formulas for common shapes are relatively simple, understanding how to adapt these techniques for irregular shapes and applying them to three-dimensional objects requires careful consideration and a solid grasp of geometric principles. By mastering these methods, you can confidently tackle a wide range of area-related calculations in various fields. Remember, precision in measurements is key to obtaining accurate results in all applications. Accurate base area calculation is the foundation for many more complex calculations involving volume and surface area.
Latest Posts
Latest Posts
-
How Is Photosynthesis And Cellular Respiration Different
Apr 03, 2025
-
Which Of The Following Is Strongest Acid
Apr 03, 2025
-
Are Prime Numbers Even Or Odd
Apr 03, 2025
-
What Is 104 Degrees Fahrenheit In Celsius
Apr 03, 2025
-
Fossil Fuels Are Classified As Non Renewable Because They
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about How Do You Find The Base Area . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
