Highest Common Factor Of 6 And 9
Juapaving
Apr 02, 2025 · 6 min read
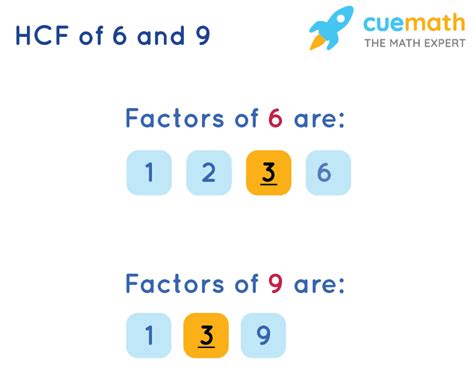
Table of Contents
Finding the Highest Common Factor (HCF) of 6 and 9: A Comprehensive Guide
The highest common factor (HCF), also known as the greatest common divisor (GCD), is the largest number that divides exactly into two or more numbers without leaving a remainder. Understanding how to find the HCF is fundamental in various mathematical fields, from simplifying fractions to solving more complex algebraic problems. This comprehensive guide will explore different methods for determining the HCF of 6 and 9, providing a detailed explanation of each approach and emphasizing the underlying mathematical concepts.
Understanding the Concept of Highest Common Factor
Before diving into the methods, let's solidify our understanding of the HCF. The HCF is essentially the largest number that is a common factor of two or more given numbers. A factor is a number that divides another number without leaving a remainder. For example, the factors of 6 are 1, 2, 3, and 6, while the factors of 9 are 1, 3, and 9.
The common factors of 6 and 9 are the numbers that appear in both lists of factors. In this case, the common factors are 1 and 3. The highest common factor is the largest among these common factors, which is 3. Therefore, the HCF of 6 and 9 is 3.
Method 1: Listing Factors
This is the most straightforward method, especially for smaller numbers. It involves listing all the factors of each number and then identifying the largest common factor.
Steps:
- List the factors of 6: 1, 2, 3, 6
- List the factors of 9: 1, 3, 9
- Identify the common factors: 1 and 3
- Determine the highest common factor: 3
This method is simple and intuitive, making it excellent for introducing the concept of HCF to beginners. However, for larger numbers, this method can become cumbersome and time-consuming.
Method 2: Prime Factorization
Prime factorization involves expressing a number as a product of its prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself (e.g., 2, 3, 5, 7, 11). This method is more efficient than listing factors, particularly for larger numbers.
Steps:
- Find the prime factorization of 6: 2 x 3
- Find the prime factorization of 9: 3 x 3
- Identify the common prime factors: 3
- Multiply the common prime factors: 3 (Since there's only one common prime factor, the HCF is 3)
This method is systematic and efficient. It's particularly useful for understanding the structure of numbers and their relationships. The process of prime factorization itself is a valuable mathematical skill.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the HCF of two numbers, especially when dealing with larger numbers. It's based on the principle that the HCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the HCF.
Steps:
- Start with the two numbers: 6 and 9
- Subtract the smaller number from the larger number: 9 - 6 = 3
- Replace the larger number with the result: Now we have 6 and 3.
- Repeat the subtraction: 6 - 3 = 3
- Repeat again: 3 - 3 = 0
- The HCF is the last non-zero remainder: 3
This method provides a systematic approach that's particularly beneficial when dealing with larger numbers where listing factors or prime factorization becomes less practical. Its efficiency makes it a preferred method in computer science algorithms.
Applications of Finding the HCF
The HCF has numerous applications across various mathematical domains and practical scenarios. Some key applications include:
-
Simplifying Fractions: The HCF is crucial for simplifying fractions to their lowest terms. For example, the fraction 6/9 can be simplified by dividing both the numerator and the denominator by their HCF (3), resulting in the equivalent fraction 2/3.
-
Solving Word Problems: Many word problems involving division or sharing require finding the HCF to determine the largest possible equal groups or portions. For instance, if you have 6 apples and 9 oranges, and you want to divide them into equal groups without any leftovers, you would need to find the HCF to determine the maximum number of groups you can make.
-
Algebraic Simplifications: The HCF is essential in simplifying algebraic expressions, particularly when dealing with polynomials. Factoring out the HCF allows for easier manipulation and simplification of algebraic expressions.
-
Geometry and Measurement: The HCF finds application in problems involving lengths, areas, or volumes. For example, finding the largest square tile that can be used to completely cover a rectangular floor without any cuts requires finding the HCF of the length and width of the floor.
-
Cryptography: Concepts related to HCF, such as modular arithmetic and prime factorization, play a vital role in various cryptographic algorithms used for secure data transmission and encryption.
Beyond 6 and 9: Extending the Concepts
While this guide focuses on finding the HCF of 6 and 9, the principles and methods discussed can be applied to any pair (or set) of numbers. Let's consider a more complex example: finding the HCF of 24 and 36.
Using Prime Factorization:
- Prime factorization of 24: 2 x 2 x 2 x 3
- Prime factorization of 36: 2 x 2 x 3 x 3
- Common prime factors: 2 x 2 x 3
- HCF: 2 x 2 x 3 = 12
Using the Euclidean Algorithm:
- 36 - 24 = 12
- 24 - 12 = 12
- 12 - 12 = 0
- HCF: 12
As you can see, both methods yield the same result. The choice of method depends on personal preference and the complexity of the numbers involved. For larger numbers, the Euclidean algorithm generally offers a more efficient solution.
Conclusion: Mastering the HCF
Understanding and applying different methods for finding the highest common factor is a cornerstone of mathematical proficiency. Whether you use the straightforward listing of factors, the systematic prime factorization method, or the efficient Euclidean algorithm, mastering these techniques equips you with valuable problem-solving skills applicable across various mathematical and practical contexts. The ability to find the HCF is not merely an academic exercise; it’s a practical tool with real-world implications in various fields. This comprehensive guide provides a solid foundation for understanding and utilizing this fundamental mathematical concept. By applying these methods and understanding the underlying principles, you can confidently tackle HCF problems of varying complexity and appreciate the significance of this seemingly simple yet powerful mathematical concept.
Latest Posts
Latest Posts
-
How Is Photosynthesis And Cellular Respiration Different
Apr 03, 2025
-
Which Of The Following Is Strongest Acid
Apr 03, 2025
-
Are Prime Numbers Even Or Odd
Apr 03, 2025
-
What Is 104 Degrees Fahrenheit In Celsius
Apr 03, 2025
-
Fossil Fuels Are Classified As Non Renewable Because They
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Highest Common Factor Of 6 And 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
