Greatest Common Factor Of 36 And 63
Juapaving
Mar 21, 2025 · 5 min read
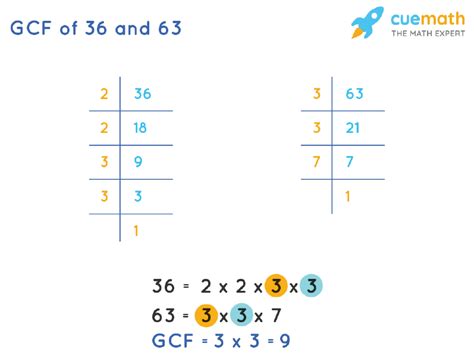
Table of Contents
Finding the Greatest Common Factor (GCF) of 36 and 63: A Comprehensive Guide
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in mathematics with applications across various fields, from simplifying fractions to solving algebraic equations. This comprehensive guide will explore different methods to determine the GCF of 36 and 63, providing a detailed explanation of each approach and highlighting their strengths and weaknesses. We’ll delve into the prime factorization method, the Euclidean algorithm, and the listing factors method, comparing their effectiveness and illustrating their application with real-world examples. By the end of this article, you'll have a robust understanding of how to find the GCF and be able to apply this knowledge to a wide range of mathematical problems.
Understanding the Greatest Common Factor (GCF)
Before we embark on calculating the GCF of 36 and 63, let's establish a clear understanding of what the GCF represents. The GCF of two or more numbers is the largest number that divides each of them without leaving a remainder. In simpler terms, it's the biggest number that fits perfectly into both numbers. Understanding this concept is crucial for solving problems involving fractions, simplifying expressions, and even tackling more advanced mathematical concepts.
Method 1: Prime Factorization
The prime factorization method involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves. Once we have the prime factorization of both numbers, we identify the common prime factors and multiply them to find the GCF.
Steps:
-
Find the prime factorization of 36: 36 = 2 x 2 x 3 x 3 = 2² x 3²
-
Find the prime factorization of 63: 63 = 3 x 3 x 7 = 3² x 7
-
Identify common prime factors: Both 36 and 63 share two factors of 3 (3²).
-
Multiply the common prime factors: 3 x 3 = 9
Therefore, the GCF of 36 and 63 is 9.
This method is particularly useful for understanding the fundamental structure of numbers and their relationships. It's also relatively easy to visualize and understand, making it a good starting point for learning about GCFs. However, for very large numbers, the prime factorization process can become quite lengthy and cumbersome.
Method 2: Listing Factors
This method involves listing all the factors of each number and then identifying the largest factor common to both.
Steps:
-
List the factors of 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
-
List the factors of 63: 1, 3, 7, 9, 21, 63
-
Identify common factors: The common factors of 36 and 63 are 1, 3, and 9.
-
Determine the greatest common factor: The largest common factor is 9.
Therefore, the GCF of 36 and 63 is 9.
The listing factors method is straightforward and intuitive, especially for smaller numbers. However, it becomes less efficient as the numbers increase in size because listing all the factors can be time-consuming and prone to errors. This method is best suited for smaller numbers where the factors are easily identifiable.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, particularly useful for larger numbers where prime factorization becomes less practical. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Steps:
-
Start with the larger number (63) and the smaller number (36).
-
Divide the larger number by the smaller number and find the remainder: 63 ÷ 36 = 1 with a remainder of 27.
-
Replace the larger number with the smaller number (36) and the smaller number with the remainder (27).
-
Repeat the process: 36 ÷ 27 = 1 with a remainder of 9.
-
Repeat again: 27 ÷ 9 = 3 with a remainder of 0.
-
The last non-zero remainder is the GCF. In this case, the last non-zero remainder is 9.
Therefore, the GCF of 36 and 63 is 9.
The Euclidean algorithm is significantly more efficient than the prime factorization method for larger numbers because it avoids the need to find all prime factors. Its iterative nature makes it suitable for implementation in computer programs.
Applications of Finding the GCF
The ability to find the GCF has far-reaching applications in various mathematical and real-world scenarios. Here are a few examples:
-
Simplifying Fractions: Finding the GCF of the numerator and denominator allows you to simplify fractions to their lowest terms. For example, the fraction 36/63 can be simplified to 4/7 by dividing both the numerator and the denominator by their GCF, which is 9.
-
Solving Algebraic Equations: GCF is crucial in factoring algebraic expressions, which is a fundamental step in solving many algebraic equations.
-
Geometry Problems: Determining the dimensions of objects with common factors often involves finding the GCF. For instance, if you need to divide a rectangular area with dimensions 36 units by 63 units into equal square sections, the GCF (9) will determine the size of each square.
-
Dividing Objects Equally: If you want to divide 36 apples and 63 oranges into the largest possible equal groups without any leftovers, the GCF (9) tells you that you can create 9 groups, each containing 4 apples and 7 oranges.
Choosing the Right Method
The best method for finding the GCF depends on the size of the numbers involved and your comfort level with different mathematical concepts.
-
For small numbers: The listing factors method is simple and intuitive.
-
For larger numbers: The Euclidean algorithm is significantly more efficient.
-
For understanding the fundamental structure of numbers: Prime factorization provides valuable insight.
Conclusion
Finding the greatest common factor of 36 and 63, whether using prime factorization, listing factors, or the Euclidean algorithm, consistently yields the same result: 9. Mastering these methods equips you with essential tools for simplifying fractions, solving equations, and tackling a variety of mathematical problems. Understanding the strengths and weaknesses of each approach empowers you to choose the most efficient method for any given situation, ultimately enhancing your problem-solving capabilities. The ability to efficiently calculate the GCF is a fundamental skill that extends beyond the classroom, proving invaluable in various practical applications. The more you practice, the more proficient and confident you will become in tackling GCF problems of any complexity.
Latest Posts
Latest Posts
-
If The Diagonals Of A Quadrilateral Bisect Each Other
Mar 28, 2025
-
Write The Electron Configuration For A Neutral Atom Of Magnesium
Mar 28, 2025
-
Differentiate Between Chemical Reaction And Nuclear Reaction
Mar 28, 2025
-
Is 35 A Multiple Of 5
Mar 28, 2025
-
Which Expression Represents The Area Of The Rectangle
Mar 28, 2025
Related Post
Thank you for visiting our website which covers about Greatest Common Factor Of 36 And 63 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
