Find The Ratio Of Their Perimeters
Juapaving
Apr 02, 2025 · 5 min read
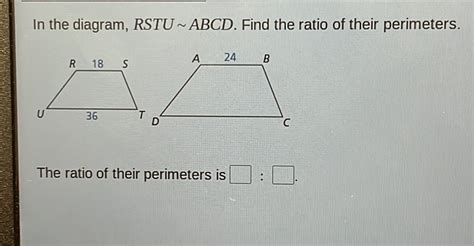
Table of Contents
Finding the Ratio of Perimeters: A Comprehensive Guide
Understanding ratios and perimeters is fundamental in geometry and problem-solving. This in-depth guide will explore various scenarios involving finding the ratio of perimeters of different shapes, from simple polygons to more complex figures. We'll delve into the underlying principles, provide step-by-step solutions to diverse examples, and equip you with the tools to tackle similar problems confidently.
What is a Ratio?
Before diving into perimeters, let's clarify the concept of a ratio. A ratio is a comparison of two or more quantities. It shows the relative sizes of the quantities. Ratios can be expressed in several ways:
- Using the colon symbol: a:b
- As a fraction: a/b
- In words: "a to b"
For instance, if we have 3 red balls and 5 blue balls, the ratio of red balls to blue balls is 3:5, or 3/5.
What is Perimeter?
The perimeter of a two-dimensional shape is the total distance around its outer boundary. It's essentially the sum of the lengths of all the sides of the shape. Calculating the perimeter depends on the shape's type:
- Rectangle: Perimeter = 2(length + width)
- Square: Perimeter = 4 × side
- Triangle: Perimeter = side1 + side2 + side3
- Circle: Perimeter (circumference) = 2πr (where 'r' is the radius)
Finding the Ratio of Perimeters: Simple Shapes
Let's start with straightforward examples involving simple geometric shapes.
Example 1: Two Rectangles
Consider two rectangles, Rectangle A and Rectangle B. Rectangle A has a length of 6 cm and a width of 4 cm. Rectangle B has a length of 9 cm and a width of 6 cm. Find the ratio of their perimeters.
Solution:
- Calculate the perimeter of Rectangle A: Perimeter A = 2(6 + 4) = 20 cm
- Calculate the perimeter of Rectangle B: Perimeter B = 2(9 + 6) = 30 cm
- Find the ratio: Ratio = Perimeter A : Perimeter B = 20:30 = 2:3
Therefore, the ratio of the perimeters of Rectangle A to Rectangle B is 2:3.
Example 2: Two Squares
Square X has sides of 5 cm, and Square Y has sides of 10 cm. Find the ratio of their perimeters.
Solution:
- Perimeter of Square X: 4 * 5 cm = 20 cm
- Perimeter of Square Y: 4 * 10 cm = 40 cm
- Ratio of perimeters: 20 cm : 40 cm = 1:2
The ratio of the perimeters of Square X to Square Y is 1:2.
Example 3: Similar Triangles
Two triangles, Triangle P and Triangle Q, are similar. The sides of Triangle P are 3 cm, 4 cm, and 5 cm. The corresponding sides of Triangle Q are 6 cm, 8 cm, and 10 cm. Find the ratio of their perimeters.
Solution:
- Perimeter of Triangle P: 3 + 4 + 5 = 12 cm
- Perimeter of Triangle Q: 6 + 8 + 10 = 24 cm
- Ratio of perimeters: 12 cm : 24 cm = 1:2
The ratio of the perimeters of similar triangles P and Q is 1:2. Note that in similar shapes, the ratio of corresponding sides is equal to the ratio of their perimeters.
Finding the Ratio of Perimeters: More Complex Scenarios
Let's move on to more challenging problems.
Example 4: Combining Shapes
A figure is composed of a square with sides of 8 cm and an equilateral triangle with sides of 8 cm attached to one side of the square. Find the perimeter of the combined figure. If another similar figure is created with sides twice the size, what is the ratio of the perimeters of the two figures?
Solution:
-
Perimeter of the first figure: The square contributes 3 sides (8cm x 3 = 24cm) and the triangle contributes 3 sides (8cm x 3 = 24cm). Total perimeter = 24cm + 24cm = 48cm.
-
Perimeter of the second figure: The sides of the square and the triangle are doubled (16cm). The square contributes 3 sides (16cm x 3 = 48cm) and the triangle contributes 3 sides (16cm x 3 = 48cm). Total perimeter = 48cm + 48cm = 96cm
-
Ratio of perimeters: 48cm : 96cm = 1:2
The ratio of the perimeters is 1:2. This illustrates that when the dimensions of similar figures are scaled up by a factor, their perimeters are scaled up by the same factor.
Example 5: Circles
Circle A has a radius of 5 cm, and Circle B has a radius of 10 cm. What is the ratio of their perimeters (circumferences)?
Solution:
- Circumference of Circle A: 2π(5) = 10π cm
- Circumference of Circle B: 2π(10) = 20π cm
- Ratio of circumferences: 10π : 20π = 1:2
The ratio of the circumferences of Circle A and Circle B is 1:2. Similar to the previous examples, scaling the radius by a factor affects the circumference by the same factor.
Example 6: Irregular Polygons
Imagine two irregular pentagons. Pentagon P has sides of 2, 3, 4, 5, and 6 cm. Pentagon Q has sides of 4, 6, 8, 10, and 12 cm. Find the ratio of their perimeters.
Solution:
- Perimeter of Pentagon P: 2 + 3 + 4 + 5 + 6 = 20 cm
- Perimeter of Pentagon Q: 4 + 6 + 8 + 10 + 12 = 40 cm
- Ratio of perimeters: 20 cm : 40 cm = 1:2
The ratio of the perimeters is 1:2. Notice that the sides of Pentagon Q are twice the length of the corresponding sides of Pentagon P.
Applying the Concept: Real-World Applications
Understanding ratios of perimeters has practical applications in various fields:
- Architecture and Engineering: Scaling blueprints and models.
- Cartography: Determining the scale of maps.
- Graphic Design: Resizing images and maintaining proportions.
- Manufacturing: Scaling up or down the dimensions of products.
Conclusion
Finding the ratio of perimeters involves understanding the concept of ratios and calculating the perimeter of different shapes. While straightforward for simple shapes, it requires careful consideration for complex figures. Remember that for similar shapes, the ratio of their perimeters is directly proportional to the ratio of their corresponding sides. This knowledge is invaluable across diverse fields, highlighting the practical significance of this geometrical concept. By mastering these techniques, you'll be well-equipped to tackle a wide range of geometry problems and real-world applications involving perimeter ratios.
Latest Posts
Latest Posts
-
1 Out Of 10 As A Percentage
Apr 03, 2025
-
How Are Prokaryotes And Eukaryotes Alike
Apr 03, 2025
-
Which Of The Following Statements Is Always True
Apr 03, 2025
-
Balanced Chemical Equation For Magnesium Oxide
Apr 03, 2025
-
What Is The Group Of Birds Called
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Find The Ratio Of Their Perimeters . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
