Does A Point Have A Dimension
Juapaving
Mar 27, 2025 · 6 min read
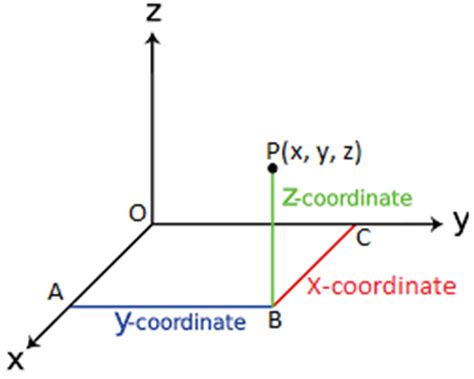
Table of Contents
Does a Point Have a Dimension? Unraveling the Mysteries of Dimensionality
The question of whether a point has a dimension is a deceptively simple one that delves deep into the foundations of geometry and mathematics. At first glance, the answer seems obvious: a point is dimensionless, lacking length, width, or height. However, a closer examination reveals a more nuanced understanding of dimensionality, challenging our intuitive grasp of space and its constituents. This article will explore the concept of dimensionality, examine the properties of points within various geometrical frameworks, and discuss the philosophical implications of defining dimensionality.
Understanding Dimensionality: Beyond the Obvious
Dimensionality, in its simplest form, refers to the number of independent coordinates needed to specify the location of a point within a space. We are most familiar with three spatial dimensions: length, width, and height. These dimensions allow us to describe the position of any object in our everyday world. However, the concept of dimensionality extends far beyond our three-dimensional experience.
One-Dimensional Space: The Line
A line is a one-dimensional object. To specify the location of a point on a line, only one coordinate is necessary. This coordinate typically represents the distance from a designated origin. Think of a number line: each point is uniquely identified by a single number.
Two-Dimensional Space: The Plane
A plane, like a flat sheet of paper, is a two-dimensional space. Two coordinates – typically x and y – are needed to specify the location of a point on a plane. These coordinates represent the distances from the point to two perpendicular axes.
Three-Dimensional Space: Our Everyday World
Our everyday experience resides in three-dimensional space. Three coordinates (x, y, and z) are required to uniquely define the position of a point in this space. These coordinates usually represent distances from three mutually perpendicular axes.
Higher Dimensions: Beyond Our Intuition
While our intuition struggles to visualize them, higher dimensions exist in mathematical models. Four-dimensional space, for example, requires four coordinates to specify a point's location. While we can't perceive it directly, four-dimensional space is crucial in various areas of physics, such as spacetime in Einstein's theory of relativity. The concept extends indefinitely, with n-dimensional spaces requiring n coordinates.
The Point: A Fundamental Building Block
A point, in geometry, is often described as a dimensionless object, lacking length, width, or height. It represents a location in space, but it doesn't occupy any space itself. This is a fundamental concept in Euclidean geometry and serves as the basis for constructing more complex geometric figures.
The Point's Lack of Extent
The crucial characteristic of a point is its lack of extent. It has no measurable size. This contrasts sharply with lines, which possess length, planes, which have both length and width, and solids, which have length, width, and height. The point is purely positional; it indicates a specific location but doesn't occupy any volume.
The Point as a Limiting Case
Another way to understand a point is as a limiting case. Imagine shrinking a square. As its sides approach zero, the square becomes indistinguishable from a point. Similarly, shrinking a cube leads to a point as its dimensions converge to zero. This perspective emphasizes the point's role as the fundamental building block from which more complex geometric figures are constructed.
Dimensionality of a Point: The Debate
While the intuitive notion suggests a point is dimensionless, the mathematical treatment can be more nuanced. The definition of dimensionality itself becomes crucial.
Zero-Dimensional?
The most common understanding is that a point is zero-dimensional. This aligns with the intuitive understanding that a point lacks any extent. It has no length, width, or height, and therefore zero dimensions according to the standard definition.
Fractal Dimension: A Different Perspective
Fractal geometry introduces a more complex view of dimensionality. Fractals are self-similar patterns that repeat at different scales. They often exhibit fractional dimensions, meaning their dimensionality is not a whole number. While a point isn't itself a fractal, the concept of fractal dimension raises questions about how we define dimensionality beyond Euclidean spaces.
The Point as a Location, Not an Object
One could argue that a point doesn't inherently have a dimension; rather, it exists within a space that has dimensions. The point simply marks a location within this space. The dimensionality is a property of the space itself, not the point residing within it.
Implications for Geometry and Beyond
The dimensionality of a point has implications beyond abstract geometry.
Coordinate Systems and Mapping
Coordinate systems rely heavily on the concept of points. Points are the fundamental elements used to define lines, planes, and higher-dimensional spaces. Their lack of extent ensures that the coordinates are uniquely assigned to locations without overlap.
Computer Graphics and Modeling
In computer graphics, points are the basic building blocks used to construct models and images. The dimensionality of these points is fundamental to how the computer interprets and displays these visual representations.
Topology and Set Theory
Topology, the study of shapes and spaces that are preserved under continuous deformations, treats points as fundamental entities. Set theory, on which topology is built, similarly uses points as fundamental elements in defining sets and spaces.
The Philosophical Significance
The question of a point's dimensionality touches upon fundamental philosophical questions about space, existence, and the nature of reality.
The Nature of Space
The existence and characteristics of points inform our understanding of space itself. If points are dimensionless, what does that imply about the structure of the space they inhabit? This question is closely related to discussions in physics and cosmology about the nature of spacetime.
The Limits of Our Intuition
Our intuitive understanding of dimensionality is limited by our three-dimensional experience. The concept of zero-dimensionality, in the context of points, challenges our intuitive grasp of space and its constituents.
Mathematical Abstraction vs. Physical Reality
The concept of a point is primarily a mathematical abstraction. While we use points to model physical objects, a perfectly dimensionless point doesn't exist in the physical world. The difference between mathematical abstraction and physical reality underscores the limitations and power of mathematical models.
Conclusion: A Multifaceted Perspective
The question of whether a point has a dimension doesn't have a simple, universally accepted answer. The intuitive understanding suggests zero dimensionality, aligning with the definition of dimensionality as the number of coordinates required to specify a location. However, considerations of fractal geometry and the philosophical implications of the concept broaden our understanding. The point, in essence, serves as a foundational element in geometry and mathematics, its dimensionality more a matter of perspective and definition than an inherent property. Ultimately, the debate highlights the rich interplay between intuitive understanding, mathematical formalism, and the philosophical underpinnings of geometry and the nature of space itself. Its continuous exploration furthers our comprehension of the fundamental building blocks of the universe and our representation thereof.
Latest Posts
Latest Posts
-
Square Root Of 30 In Radical Form
Mar 30, 2025
-
5 Letter Words Starting With Cor
Mar 30, 2025
-
What Are The Factor Pairs Of 100
Mar 30, 2025
-
What Can You Multiply To Get 72
Mar 30, 2025
-
Write The Electron Configuration For A Neutral Atom Of Oxygen
Mar 30, 2025
Related Post
Thank you for visiting our website which covers about Does A Point Have A Dimension . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
