What Are The Factor Pairs Of 100
Juapaving
Mar 30, 2025 · 5 min read
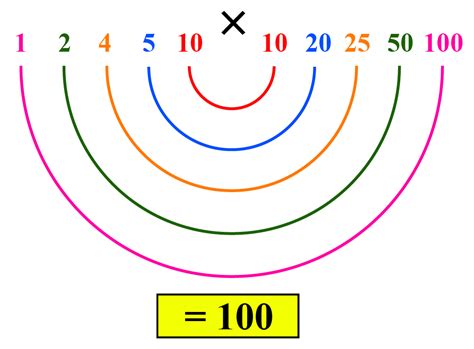
Table of Contents
What Are the Factor Pairs of 100? A Deep Dive into Number Theory
Finding the factor pairs of a number is a fundamental concept in number theory and arithmetic. It's a stepping stone to understanding more complex mathematical ideas like prime factorization, greatest common divisors (GCD), and least common multiples (LCM). This article delves into the factor pairs of 100, explaining the process of finding them, their significance, and extending the concept to broader mathematical applications. We'll explore different approaches, making this topic accessible to everyone from elementary school students to those refreshing their mathematical skills.
Understanding Factors and Factor Pairs
Before we jump into finding the factor pairs of 100, let's define what factors and factor pairs actually are.
Factors: Factors of a number are whole numbers that divide the number evenly without leaving a remainder. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12 because each of these numbers divides 12 perfectly.
Factor Pairs: Factor pairs are sets of two factors whose product equals the given number. For 12, the factor pairs are (1, 12), (2, 6), and (3, 4). Notice that the order within the pair matters; (2, 6) is different from (6, 2) even though they contain the same factors.
Finding the Factor Pairs of 100: A Systematic Approach
There are several ways to find the factor pairs of 100. Let's explore two common methods:
Method 1: Systematic Listing
This method involves systematically listing all the factors of 100 and then pairing them up. We start by considering the smallest factor, 1:
- Start with 1: 1 x 100 = 100, so (1, 100) is a factor pair.
- Check the next whole number: 2 x 50 = 100, yielding (2, 50).
- Continue checking: 4 x 25 = 100, giving us (4, 25).
- Progress systematically: 5 x 20 = 100, resulting in (5, 20).
- Moving upwards: 10 x 10 = 100, giving us (10, 10). Notice this is a special case where the pair contains the same number.
At this point, we've exhausted all factors. If we continued beyond 10, we would simply repeat the pairs in reverse order (20, 5), (25, 4), (50, 2), (100, 1).
Therefore, the factor pairs of 100 are: (1, 100), (2, 50), (4, 25), (5, 20), and (10, 10).
Method 2: Prime Factorization
This method uses the prime factorization of the number to find its factors. Prime factorization is expressing a number as a product of its prime factors (numbers divisible only by 1 and themselves).
The prime factorization of 100 is 2 x 2 x 5 x 5, or 2² x 5².
Using this prime factorization, we can systematically generate the factors:
-
Use the exponents: The exponents in the prime factorization are 2 and 2 (for 2 and 5 respectively). Add 1 to each exponent: 2 + 1 = 3 and 2 + 1 = 3. Multiply these results: 3 x 3 = 9. This tells us there are 9 total factors.
-
List the factors: From the prime factorization, we can generate all possible factors by combining the prime factors in different ways:
- 2⁰ x 5⁰ = 1
- 2¹ x 5⁰ = 2
- 2² x 5⁰ = 4
- 2⁰ x 5¹ = 5
- 2¹ x 5¹ = 10
- 2² x 5¹ = 20
- 2⁰ x 5² = 25
- 2¹ x 5² = 50
- 2² x 5² = 100
-
Form the pairs: Now that we have all the factors, we can pair them up to find the factor pairs, arriving at the same result as Method 1: (1, 100), (2, 50), (4, 25), (5, 20), (10, 10).
The Significance of Factor Pairs
Understanding factor pairs is crucial for several mathematical concepts and real-world applications:
- Simplifying Fractions: Finding the greatest common factor (GCF) of the numerator and denominator of a fraction allows you to simplify it to its lowest terms. The GCF is found by looking at the common factors, often identified through factor pairs.
- Solving Equations: Factor pairs can be useful in solving quadratic equations by factoring the expression.
- Area and Volume Calculations: Factor pairs can help in determining the dimensions of rectangles and rectangular prisms given their area or volume.
- Combinatorics and Probability: In problems involving combinations and probability, understanding factors and their pairs can be essential in calculating different possibilities.
- Number Theory: Factor pairs are fundamental in many areas of number theory, such as exploring perfect numbers, amicable numbers, and other number properties.
Extending the Concept: Factor Pairs of Other Numbers
The techniques we used to find the factor pairs of 100 are applicable to any whole number. Let's consider a few examples:
Factor Pairs of 24:
- Systematic Listing: (1, 24), (2, 12), (3, 8), (4, 6)
- Prime Factorization: 24 = 2³ x 3¹ (There are (3+1)(1+1) = 8 factors)
Factor Pairs of 36:
- Systematic Listing: (1, 36), (2, 18), (3, 12), (4, 9), (6, 6)
- Prime Factorization: 36 = 2² x 3² (There are (2+1)(2+1) = 9 factors)
Factor Pairs of 144:
- Systematic Listing: This becomes more tedious with larger numbers.
- Prime Factorization: 144 = 2⁴ x 3² (There are (4+1)(2+1) = 15 factors) This method is significantly more efficient.
Conclusion: Mastering Factor Pairs
Finding the factor pairs of a number, as illustrated with the example of 100, is a foundational skill in mathematics. Both the systematic listing and prime factorization methods provide effective ways to achieve this. Understanding factor pairs unlocks a deeper appreciation of number theory and facilitates problem-solving in various mathematical contexts and real-world applications. By mastering this concept, you build a solid foundation for more advanced mathematical explorations. Remember, practice makes perfect – try finding the factor pairs of various numbers to solidify your understanding. The more you practice, the faster and more efficiently you'll be able to identify factor pairs for any given number. This skill, while seemingly simple, is a powerful tool in your mathematical toolbox.
Latest Posts
Latest Posts
-
Whats The Difference Between Electron Geometry And Molecular Geometry
Apr 01, 2025
-
Which Is Not A Nucleotide Found In Dna
Apr 01, 2025
-
5 Letter Words Starting With A S
Apr 01, 2025
-
How Many Atp Does The Electron Transport Chain Produce
Apr 01, 2025
-
When Do You Use Left Hand Rule Electromagnetism
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about What Are The Factor Pairs Of 100 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
