Common Denominator Of 7 And 5
Juapaving
Mar 25, 2025 · 6 min read
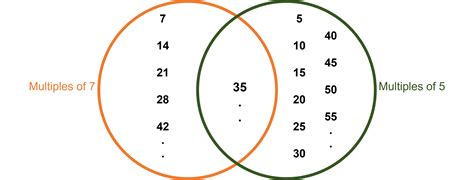
Table of Contents
Unveiling the Common Denominator: A Deep Dive into 7 and 5
Finding the common denominator of two numbers might seem like a simple arithmetic task, suitable only for elementary school. However, understanding the underlying principles and exploring the broader implications of this seemingly basic concept opens up a fascinating world of number theory and its applications in various fields. This article will delve deep into finding the common denominator of 7 and 5, exploring the concept's nuances, practical applications, and its connection to more advanced mathematical ideas.
What is a Common Denominator?
Before we tackle the specific case of 7 and 5, let's establish a firm understanding of what a common denominator actually is. In mathematics, a common denominator is a shared multiple of the denominators of two or more fractions. It's the number that allows us to add, subtract, and compare fractions effectively. To illustrate, consider the fractions 1/2 and 1/3. Their denominators are 2 and 3 respectively. To add them, we need a common denominator, which is a multiple of both 2 and 3. The least common multiple (LCM) of 2 and 3 is 6, making 6 the least common denominator (LCD).
Finding the Least Common Denominator (LCD) of 7 and 5
The numbers 7 and 5 are both prime numbers. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. This characteristic simplifies the process of finding their least common denominator significantly.
Since 7 and 5 are prime and share no common factors other than 1, their least common multiple (and therefore their least common denominator) is simply their product: 7 x 5 = 35.
Therefore, the least common denominator of 7 and 5 is 35.
Why is the LCD Important?
The significance of the LCD extends far beyond the simple addition and subtraction of fractions. It plays a crucial role in various mathematical operations and real-world applications.
-
Fraction Arithmetic: As previously mentioned, the LCD is essential for adding and subtracting fractions. Without a common denominator, we cannot directly combine fractions. The LCD allows us to rewrite the fractions with equivalent values, making the addition or subtraction straightforward.
-
Comparing Fractions: When comparing fractions, the LCD helps determine which fraction is larger or smaller. By rewriting the fractions with the same denominator, we can directly compare their numerators.
-
Solving Equations: Many algebraic equations involve fractions. Finding the LCD is often a necessary step in simplifying and solving these equations. By multiplying both sides of the equation by the LCD, we can eliminate the denominators and solve for the variable more easily.
-
Ratio and Proportion Problems: Real-world problems involving ratios and proportions often require manipulating fractions. The LCD simplifies these calculations, making it easier to solve for unknown quantities.
-
Advanced Mathematics: The concept of LCM and GCD (Greatest Common Divisor) extends into more advanced areas of mathematics like abstract algebra, number theory, and cryptography. Understanding the fundamental principles of finding common denominators lays the groundwork for grasping these more complex concepts.
Beyond the Basics: Exploring Related Concepts
The concept of common denominators is closely related to several other important mathematical ideas:
-
Least Common Multiple (LCM): As we've seen, the LCD of two or more fractions is the LCM of their denominators. The LCM is the smallest positive integer that is a multiple of all the given numbers.
-
Greatest Common Divisor (GCD): The GCD, also known as the greatest common factor (GCF), is the largest positive integer that divides all the given numbers without leaving a remainder. While not directly involved in finding the LCD of 7 and 5 (because they are prime and their GCD is 1), the GCD is a crucial concept in number theory and is often used in conjunction with the LCM.
-
Prime Factorization: The prime factorization of a number is the expression of that number as a product of prime numbers. For composite numbers (numbers that are not prime), prime factorization is a powerful tool for finding the LCM and GCD. For example, finding the LCM of 12 and 18 involves first finding their prime factorizations (12 = 2² x 3 and 18 = 2 x 3²). The LCM is then found by taking the highest power of each prime factor present in the factorizations (LCM(12,18) = 2² x 3² = 36).
-
Euclidean Algorithm: This algorithm provides an efficient method for finding the GCD of two numbers. While less directly relevant to finding the LCD of 7 and 5 (due to their prime nature), the Euclidean algorithm is a fundamental tool in number theory and has applications in various fields, including cryptography.
Real-World Applications of Common Denominators
The practical applications of finding common denominators extend beyond the classroom:
-
Baking and Cooking: Recipes often involve fractions of ingredients. Understanding common denominators is crucial for accurately measuring and combining ingredients.
-
Construction and Engineering: Construction projects frequently require precise measurements and calculations involving fractions. The ability to work with fractions and find common denominators ensures accuracy and efficiency.
-
Finance and Accounting: Financial calculations often involve fractions, particularly when dealing with percentages, interest rates, and proportions.
-
Data Analysis: When working with data, representing values as fractions and using common denominators can aid in comparisons and interpretations.
-
Computer Science: Concepts related to LCM and GCD are utilized in computer algorithms, particularly those dealing with data structures and optimization.
Expanding the Concept: More than Two Numbers
While this article focused on the common denominator of 7 and 5, the principles discussed extend to finding the LCD for more than two numbers. The process involves finding the LCM of all the denominators involved. For example, to find the LCD of the fractions 1/6, 1/10, and 1/15, we first find the prime factorization of each denominator:
- 6 = 2 x 3
- 10 = 2 x 5
- 15 = 3 x 5
The LCM is found by taking the highest power of each prime factor present: 2 x 3 x 5 = 30. Therefore, the LCD of 1/6, 1/10, and 1/15 is 30.
Conclusion: The Power of Simplicity
The seemingly simple task of finding the common denominator of 7 and 5, which is 35, unveils a surprisingly rich mathematical landscape. Understanding this fundamental concept allows for proficiency in fraction arithmetic, problem-solving, and provides a stepping stone to more advanced mathematical concepts. The broad applications of this principle underscore its importance across various disciplines, highlighting its significance beyond the confines of the mathematics classroom. From baking a cake to solving complex engineering problems, the ability to work effectively with fractions and find common denominators remains an invaluable skill in our everyday lives and in professional endeavors. The simplicity of the concept belies its power and versatility, making it a cornerstone of mathematical understanding.
Latest Posts
Latest Posts
-
9 Rounded To The Nearest Tenth
Mar 27, 2025
-
What Percent Is 15 Of 50
Mar 27, 2025
-
Nh4 3po4 Pb No3 4 Pb3 Po4 4 Nh4no3
Mar 27, 2025
-
In Which Figure Is Point G A Centroid
Mar 27, 2025
-
What Is The Charge Of Beryllium
Mar 27, 2025
Related Post
Thank you for visiting our website which covers about Common Denominator Of 7 And 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
