In Which Figure Is Point G A Centroid
Juapaving
Mar 27, 2025 · 5 min read
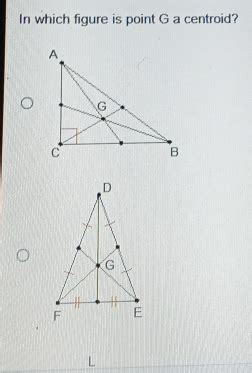
Table of Contents
In Which Figure is Point G a Centroid? A Comprehensive Guide
Understanding centroids is crucial in various fields, from geometry and engineering to computer graphics and data analysis. This comprehensive guide dives deep into the concept of a centroid, explaining what it is, how to identify it in different geometric figures, and providing practical examples to solidify your understanding.
What is a Centroid?
A centroid is the geometric center of a figure. It's the point where the figure would balance perfectly if it were a physical object with uniform density. Think of it as the average position of all the points within the figure. While the term is often used interchangeably with "center of mass" (especially in physics), there's a subtle difference: the center of mass considers the density distribution, whereas the centroid assumes uniform density. For figures with uniform density, the centroid and center of mass coincide.
Finding the centroid involves calculating the average of the coordinates of all points in the figure. However, direct calculation can be cumbersome for complex shapes. Fortunately, there are simpler methods for common geometric figures.
Centroids of Common Geometric Figures
Let's explore how to locate the centroid for various shapes:
1. Triangle
The centroid of a triangle is the point of intersection of its medians. A median is a line segment connecting a vertex to the midpoint of the opposite side. Importantly, a triangle always has exactly one centroid, and it's always located inside the triangle.
How to find it: Draw any two medians; their intersection is the centroid. Alternatively, you can use the coordinates of the vertices. If the vertices are A(x₁, y₁), B(x₂, y₂), and C(x₃, y₃), the centroid G has coordinates:
G(x, y) = ((x₁ + x₂ + x₃)/3, (y₁ + y₂ + y₃)/3)
This formula elegantly shows the centroid as the average of the vertices' coordinates.
2. Rectangle
For a rectangle, the centroid is simply the intersection of its diagonals. This point is also the midpoint of the rectangle. If the vertices are A(0, b), B(a, b), C(a, 0), and D(0, 0), the centroid G is located at:
G(x, y) = (a/2, b/2)
This intuitively makes sense: it's the middle point of the rectangle.
3. Square
As a special case of a rectangle, a square's centroid is also the intersection of its diagonals and the midpoint of the square. The simplicity arises from the square's symmetry.
4. Parallelogram
In a parallelogram, the centroid is the intersection point of its diagonals. Similar to the rectangle, this point is also the midpoint of the parallelogram.
5. Regular Polygon
For regular polygons (like a pentagon, hexagon, etc.), the centroid is located at the geometric center of the polygon. This is the point equidistant from all vertices and all sides. The centroid for a regular polygon is the same as its center of symmetry.
6. Circle & Ellipse
The centroid of a circle or an ellipse is its center. This is a direct consequence of their rotational symmetry.
7. Irregular Shapes
Finding the centroid of irregular shapes is more challenging. Numerical integration techniques or approximations using computer software are often necessary. These methods involve dividing the irregular shape into smaller, simpler shapes, calculating the centroids of those shapes, and then weighting their contributions based on their areas. Methods like the method of moments are commonly used.
Applications of Centroids
Understanding centroids has far-reaching applications:
- Engineering: Centroid calculations are essential in structural engineering for determining the center of gravity of structures, crucial for stability and load distribution.
- Physics: Centroids help in calculating the center of mass, important for analyzing the motion and equilibrium of objects.
- Computer Graphics: Centroids are used in image processing and computer-aided design (CAD) for object manipulation and transformations.
- Data Analysis: In data visualization, the centroid can represent the "average" location of data points in a dataset.
- Architecture: Centroids are critical for structural design in buildings to ensure stability and safety.
- Manufacturing: In manufacturing, knowing the centroid is crucial for balancing rotating parts and minimizing vibrations.
Identifying Point G as a Centroid: Examples and Problem Solving
Let's look at specific examples to illustrate how to identify when a point G is a centroid:
Example 1:
Imagine a triangle ABC with vertices A(1, 2), B(4, 6), and C(7, 2). A point G is given as (4, ⅓(2+6+2)) = (4, 10/3). Is G the centroid?
Using the centroid formula: G(x, y) = ((1 + 4 + 7)/3, (2 + 6 + 2)/3) = (4, 10/3). Therefore, G is the centroid of triangle ABC.
Example 2:
Consider a rectangle with vertices (0,0), (5,0), (5,3), and (0,3). Point G is located at (2.5, 1.5). Is G the centroid?
The centroid of a rectangle is at (a/2, b/2), where a and b are the side lengths. In this case, a = 5 and b = 3, so the centroid is (5/2, 3/2) = (2.5, 1.5). Therefore, G is the centroid.
Example 3:
A point G is given within a complex irregular shape. Determining if G is the centroid requires using numerical methods to calculate the centroid and comparing its coordinates with the coordinates of point G. Software or advanced mathematical techniques would be necessary.
Advanced Concepts and Further Exploration
For more complex scenarios, consider these advanced topics:
- Composite figures: Determining the centroid of a figure composed of multiple simpler shapes.
- Theorems of Pappus: Relating the volume and surface area of a solid of revolution to the centroid of the generating curve.
- Centroids of curves: Finding the centroid of a curve instead of a planar area.
- Numerical methods for centroid calculation: Techniques like the trapezoidal rule and Simpson's rule can approximate the centroid of irregular shapes.
By understanding the fundamentals of centroids and applying the appropriate methods for different geometric figures, you can confidently identify when a point G represents the geometric center of a shape. Remember, the centroid is a fundamental concept with broad implications across various disciplines, making its understanding crucial for anyone working with geometric figures or spatial data. Mastering this concept will enhance your problem-solving skills and broaden your understanding of geometry and its applications.
Latest Posts
Latest Posts
-
Who First Used The Term Cell
Mar 30, 2025
-
Light Energy Is Converted To Chemical Energy In The
Mar 30, 2025
-
How Do You Add Scientific Notation
Mar 30, 2025
-
Solving Systems Of Equations By Elimination Solver
Mar 30, 2025
-
What Is The Valence Value Of Carbon
Mar 30, 2025
Related Post
Thank you for visiting our website which covers about In Which Figure Is Point G A Centroid . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
