Can A Scalene Triangle Be Obtuse
Juapaving
Apr 06, 2025 · 5 min read
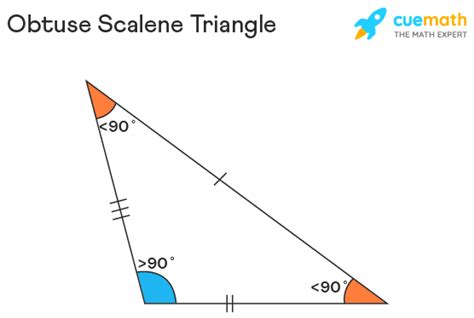
Table of Contents
Can a Scalene Triangle Be Obtuse? Exploring the Geometry of Triangles
The world of geometry often presents intriguing questions that challenge our understanding of shapes and their properties. One such question that frequently arises involves the relationship between different types of triangles: can a scalene triangle be obtuse? The answer, as we'll explore in detail, is a resounding yes. This article will delve deep into the definitions of scalene and obtuse triangles, explore their properties, and provide numerous examples to solidify your understanding. We will also examine how these concepts relate to other triangle classifications, such as acute and right triangles.
Understanding the Definitions: Scalene and Obtuse Triangles
Before we can answer our central question, let's clearly define the terms involved:
Scalene Triangle: A Triangle with No Equal Sides
A scalene triangle is defined by its sides. Specifically, it possesses the characteristic of having three sides of unequal lengths. This means that no two sides of a scalene triangle are congruent (equal in length). This unique property distinguishes it from other triangle types like isosceles (two equal sides) and equilateral (three equal sides). The angles within a scalene triangle are also always unequal.
Obtuse Triangle: A Triangle with One Obtuse Angle
An obtuse triangle is defined by its angles. It is characterized by the presence of one obtuse angle, meaning an angle greater than 90 degrees but less than 180 degrees. The other two angles in an obtuse triangle must be acute angles (less than 90 degrees). The sum of the angles in any triangle, regardless of its type, always equals 180 degrees. This fundamental property of triangles is crucial when analyzing and classifying them.
The Interplay of Scalene and Obtuse Properties
The key to understanding whether a scalene triangle can be obtuse lies in realizing that the side lengths and angles are related but independent properties. While the lengths of the sides determine the angles, and vice versa, the conditions for being a scalene triangle and an obtuse triangle are not mutually exclusive.
Let's break this down:
- Scalene: Focuses solely on the unequal lengths of the three sides.
- Obtuse: Focuses solely on the presence of one angle greater than 90 degrees.
A triangle can satisfy both conditions simultaneously. The unequal side lengths do not prohibit the existence of an obtuse angle.
Examples of Obtuse Scalene Triangles
To further solidify the concept, let's consider some examples. It's often easiest to visualize this with concrete numerical examples:
Example 1:
Imagine a triangle with sides of length 5, 6, and 10 units. Clearly, this is a scalene triangle because all sides have different lengths. If you were to calculate the angles using the Law of Cosines or other trigonometric methods, you would find that one angle is indeed obtuse (greater than 90 degrees). Therefore, this is an example of an obtuse scalene triangle.
Example 2:
Consider a triangle with sides of length 3, 4, and 7. Again, the side lengths are all different, making it scalene. Using trigonometric methods, you'll find one angle is obtuse. This is another example of an obtuse scalene triangle.
Example 3:
Let's use slightly different numbers to demonstrate that the relationship remains consistent: Consider a triangle with sides of lengths 2, 5, and 6. This is a scalene triangle; note that the lengths are again all different. Calculations will reveal one obtuse angle, confirming that it’s an obtuse scalene triangle.
These examples highlight that the existence of an obtuse angle doesn't violate the condition of having unequal sides. The combination of both properties is perfectly possible.
Visualizing Obtuse Scalene Triangles
While numerical examples are helpful, visualizing these triangles is crucial for a complete understanding. Imagine drawing a triangle where one side is significantly longer than the other two. By carefully adjusting the angles, you can easily create a triangle with one angle greater than 90 degrees, fulfilling both the scalene and obtuse conditions. You can even use interactive geometry software to create and manipulate these triangles, allowing for a more dynamic exploration of their properties.
Distinguishing from Other Triangle Types
Understanding the relationship between scalene and obtuse triangles requires differentiating them from other triangle types:
Acute Scalene Triangles
These triangles have three unequal sides (scalene) and all three angles are acute (less than 90 degrees).
Right Scalene Triangles
These triangles have three unequal sides (scalene) and one right angle (exactly 90 degrees).
Obtuse Isosceles Triangles
These triangles have two equal sides (isosceles) and one obtuse angle.
Obtuse Equilateral Triangles
It's important to note that an obtuse equilateral triangle is impossible. An equilateral triangle, by definition, has three equal sides and three equal angles of 60 degrees each (all acute). The angles cannot be obtuse.
Practical Applications and Further Exploration
Understanding the classification of triangles, particularly the interplay between scalene and obtuse properties, is not just a theoretical exercise. It has practical applications in various fields:
- Engineering: The design of structures often involves calculations involving triangles, and understanding their properties is crucial for stability and efficiency.
- Computer Graphics: In 3D modeling and animation, accurately representing triangles and their properties is essential for creating realistic images.
- Cartography: The triangulation method, used in surveying and mapping, relies on the properties of triangles to determine distances and positions.
Further exploration into the topic could involve investigating the trigonometric relationships within obtuse scalene triangles, proving geometric theorems related to these shapes, or exploring more complex geometric problems involving these types of triangles. The possibilities are abundant, offering a rich learning experience for those interested in geometry.
Conclusion: A Definitive Yes
The question "Can a scalene triangle be obtuse?" is definitively answered with a yes. The properties of having unequal sides (scalene) and possessing one obtuse angle are not mutually exclusive. Many examples illustrate this, both numerically and visually. Understanding this relationship is fundamental to a comprehensive understanding of triangle geometry and its applications in various fields. We've explored examples, visualizations, and distinctions from other triangle types to provide a comprehensive understanding of this important geometrical concept. The exploration of this seemingly simple question opens up a world of geometric possibilities and practical applications.
Latest Posts
Latest Posts
-
Why Is Sigma Bond Stronger Than Pi Bond
Apr 07, 2025
-
Difference Between A Square And A Rhombus
Apr 07, 2025
-
Capacity Of Doing Work Is Called
Apr 07, 2025
-
Is Ascending Order A To Z
Apr 07, 2025
-
Which Number Is A Factor Of 51
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about Can A Scalene Triangle Be Obtuse . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
