Difference Between A Square And A Rhombus
Juapaving
Apr 07, 2025 · 5 min read
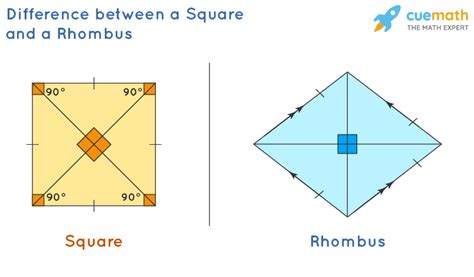
Table of Contents
Delving Deep: Unveiling the Distinctions Between Squares and Rhombuses
Squares and rhombuses, both belonging to the broader family of quadrilaterals, often cause confusion due to their shared characteristics. While seemingly similar at first glance, a closer examination reveals crucial differences that set them apart. This comprehensive guide will dissect the defining features of each shape, highlight their similarities, and finally, illuminate the key distinctions that definitively separate a square from a rhombus. Understanding these differences is crucial for anyone studying geometry, from students to professionals working with design, engineering, or architecture.
Shared Characteristics: The Family Resemblance
Before delving into their differences, let's acknowledge the common ground shared by squares and rhombuses. Both shapes are parallelograms, meaning they possess the following characteristics:
- Two pairs of parallel sides: Opposite sides are parallel to each other.
- Opposite sides are congruent: Opposite sides have equal length.
- Opposite angles are congruent: Opposite angles have equal measure.
- Consecutive angles are supplementary: The sum of any two consecutive angles is 180 degrees.
This shared foundation makes understanding the specific differences between a square and a rhombus all the more important. It's like understanding the nuanced differences between siblings who share a similar family history but have distinct personalities.
The Square: A Paragon of Symmetry
A square is a truly exceptional quadrilateral. It embodies perfect symmetry and possesses a unique set of properties that elevate it beyond a simple parallelogram. Let's explore its defining features:
Defining Features of a Square:
- Four equal sides: All four sides of a square are of equal length. This is the most fundamental characteristic defining a square.
- Four right angles: Each of the four interior angles measures exactly 90 degrees. This property contributes to the square's perfect symmetry and stability.
- Equal diagonals: The two diagonals of a square are equal in length and bisect each other at right angles. This property is not shared by all quadrilaterals.
- Diagonals bisect the angles: The diagonals of a square bisect the interior angles, dividing them into two 45-degree angles.
These properties combine to create a shape that is both visually appealing and mathematically precise. Its inherent symmetry makes it highly versatile in design and construction, lending itself to a vast range of applications.
The Rhombus: A Diamond in the Rough
The rhombus, often referred to as a diamond, shares some characteristics with the square, but falls short of its perfect symmetry. While it possesses parallel sides and congruent opposite angles like a square, it lacks the crucial right angles.
Defining Features of a Rhombus:
- Four equal sides: Like a square, all four sides of a rhombus are equal in length. This is its most prominent shared feature with the square.
- Opposite angles are congruent: Opposite angles are equal in measure, a characteristic it shares with parallelograms and squares.
- Consecutive angles are supplementary: The sum of any two consecutive angles is 180 degrees.
- Diagonals bisect each other: The diagonals of a rhombus intersect at a point that bisects both diagonals. However, unlike in a square, these diagonals are not necessarily equal in length.
- Diagonals are perpendicular bisectors: The diagonals of a rhombus intersect at right angles, perpendicularly bisecting each other. This is a key characteristic of a rhombus but its angles aren't necessarily 90 degrees like in a square.
The rhombus, while possessing its own elegance, lacks the perfect 90-degree angles of a square. This subtle difference significantly alters its geometrical properties and applications.
Key Differences: Unveiling the Distinctions
The crucial distinctions between a square and a rhombus lie in the measure of their angles and the relationship between their diagonals:
| Feature | Square | Rhombus |
|---|---|---|
| Angles | Four 90-degree angles | Opposite angles are equal, but not necessarily 90 degrees |
| Diagonals | Equal in length, bisect each other at 90 degrees, and bisect angles | Unequal in length, bisect each other at 90 degrees |
| Symmetry | Perfect rotational and reflectional symmetry | Reflectional symmetry across diagonals only |
The table above clearly highlights that while both shapes possess four equal sides, the presence of four right angles (90 degrees) is the defining characteristic distinguishing a square from a rhombus. A square is, in essence, a special type of rhombus – a rhombus with right angles. All squares are rhombuses, but not all rhombuses are squares.
Real-World Applications: Squares and Rhombuses in Action
Understanding the differences between squares and rhombuses extends beyond theoretical geometry. Their unique properties make them essential in various real-world applications:
Squares: The Foundation of Stability
Squares, due to their perfect symmetry and right angles, are the cornerstone of stable structures. Their presence is ubiquitous in:
- Architecture and Construction: Square and rectangular structures offer exceptional stability, making them ideal for buildings, bridges, and other constructions.
- Engineering: Square components are fundamental in mechanical engineering, ensuring precise alignment and reducing stress points.
- Design: Squares provide a sense of balance and order in design, used extensively in logos, packaging, and visual art.
Rhombuses: Versatility in Design and Nature
Rhombuses, with their slanted sides, offer a unique aesthetic appeal and are found in diverse applications:
- Art and Design: The diamond shape, a visual representation of a rhombus, is a recurring motif in art, jewelry, and graphic design, adding dynamism and visual interest.
- Nature: Rhombus-like structures appear in nature, exemplified by some crystalline structures and the arrangement of certain leaves and petals.
- Engineering: Certain engineering designs, particularly those involving stress distribution in non-uniform materials, utilize rhombus-shaped components.
Conclusion: Appreciating the Nuances
In conclusion, while squares and rhombuses share the commonality of four equal sides, their fundamental differences in angle measurements and diagonal properties create unique characteristics that dictate their respective applications. A square is a specialized case of a rhombus, possessing perfect symmetry and right angles that lend themselves to stable structures and precise design applications. The rhombus, with its unequal diagonals and varied angles, offers a unique aesthetic appeal and finds its place in various design and natural contexts. Understanding these distinctions is key to appreciating the richness and versatility of geometric shapes in our world. This knowledge extends far beyond the classroom, impacting fields ranging from architecture and engineering to design and art. By mastering these fundamental concepts, you are equipping yourself with the tools to navigate the intricate world of geometry with greater confidence and insight.
Latest Posts
Latest Posts
-
Orbitals That Have The Same Energy Are Called
Apr 09, 2025
-
How Many Milliamps In One Amp
Apr 09, 2025
-
An Animal That Eats Another Animal Is Called
Apr 09, 2025
-
6 928 Rounded To The Nearest Tenth
Apr 09, 2025
-
Is Salad A Mixture Or Solution
Apr 09, 2025
Related Post
Thank you for visiting our website which covers about Difference Between A Square And A Rhombus . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.