Which Number Is A Factor Of 51
Juapaving
Apr 07, 2025 · 5 min read
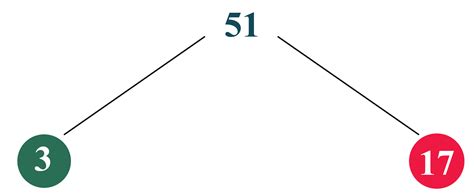
Table of Contents
Which Number is a Factor of 51? A Deep Dive into Divisibility and Prime Factorization
Finding the factors of a number is a fundamental concept in mathematics, crucial for understanding number theory, algebra, and even more advanced topics. This article explores the question, "Which number is a factor of 51?", but goes far beyond a simple answer. We'll delve into the methods for finding factors, explore the concepts of prime factorization and divisibility rules, and finally, discuss the importance of factoring in various mathematical contexts.
Understanding Factors and Divisibility
Before we pinpoint the factors of 51, let's clarify the core concepts. A factor (or divisor) of a number is a whole number that divides the number exactly, leaving no remainder. In simpler terms, if you can divide a number by another number without getting a fraction or decimal, the second number is a factor of the first. This is directly linked to the concept of divisibility. A number is divisible by another if the result of the division is a whole number.
Identifying Factors: A Systematic Approach
There are several ways to find the factors of a number. Let's explore some common methods, using 51 as our example:
-
Listing Pairs: We systematically search for pairs of numbers that multiply to give 51. We start with 1 (which is always a factor) and its pair: 1 x 51 = 51. Then we check for other pairs. Since 51 is not divisible by 2 (it's not an even number), we move on to 3. 3 x 17 = 51. We've exhausted all possible pairs since 17 is a prime number (a number divisible only by 1 and itself). Thus, the factors of 51 are 1, 3, 17, and 51.
-
Prime Factorization: This method is particularly powerful for larger numbers. Prime factorization involves expressing a number as the product of its prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. The prime factorization of 51 is 3 x 17. Once you have the prime factorization, you can easily determine all the factors by combining the prime factors in different ways. For example, the factors of 51 are 1 (1 alone), 3 (one 3), 17 (one 17), and 51 (3 x 17).
-
Divisibility Rules: These rules offer shortcuts for determining divisibility by specific numbers without performing long division. For instance, a number is divisible by 3 if the sum of its digits is divisible by 3. In the case of 51, 5 + 1 = 6, which is divisible by 3, confirming that 3 is a factor of 51. Understanding divisibility rules can significantly speed up the factor-finding process, especially for larger numbers.
The Factors of 51: A Complete List
Based on the methods discussed above, the complete list of factors of 51 is: 1, 3, 17, and 51. Each of these numbers divides 51 evenly, leaving no remainder.
Beyond 51: Exploring Factorization in Deeper Detail
The concept of factorization extends far beyond simply finding the factors of a single number. Let's explore its significance in various mathematical areas:
1. Greatest Common Factor (GCF) and Least Common Multiple (LCM):
Finding the greatest common factor (GCF) and least common multiple (LCM) of two or more numbers are common tasks in mathematics. The GCF is the largest number that divides all the given numbers without leaving a remainder. The LCM is the smallest number that is a multiple of all the given numbers. Prime factorization is a highly efficient method for calculating both GCF and LCM.
2. Simplifying Fractions:
Factorization plays a vital role in simplifying fractions. To simplify a fraction, you find the GCF of the numerator and denominator and divide both by the GCF. This process reduces the fraction to its simplest form.
3. Solving Algebraic Equations:
Factorization is a cornerstone of algebra. Factoring quadratic equations, for example, allows us to find the roots (solutions) of the equation. This technique is used extensively in various areas, including physics and engineering, for solving problems involving quadratic relationships.
4. Cryptography:
Factorization is a fundamental element in cryptography, specifically in public-key cryptography systems like RSA. The security of these systems relies on the difficulty of factoring very large numbers into their prime factors.
5. Number Theory:
The study of factors and factorization is central to number theory, a branch of mathematics focused on the properties of integers. Concepts such as perfect numbers, amicable numbers, and prime numbers are all deeply intertwined with the idea of factorization.
Practical Applications of Factorization
The ability to find factors and understand factorization extends beyond theoretical mathematics. It has practical applications in various fields:
-
Computer Science: Efficient algorithms for factorization are crucial in cryptography and database management.
-
Engineering: Factorization is used in structural engineering to analyze stresses and strains in structures.
-
Finance: Factorization techniques are applied in financial modeling and risk assessment.
-
Data Analysis: Understanding factors is important for analyzing and interpreting data in various fields.
Conclusion: The Importance of Understanding Factors
The seemingly simple question of finding the factors of 51 leads us down a path revealing the rich and multifaceted nature of factorization. From its fundamental role in simplifying fractions to its critical importance in advanced cryptographic systems, the ability to find factors and understand their significance is a fundamental skill in mathematics and has broad implications across various disciplines. By mastering the techniques discussed here, you will not only answer the question of which numbers are factors of 51 but also gain a deeper appreciation for the broader importance of factorization in the world of mathematics and beyond. The more you understand about factors, the better equipped you'll be to tackle more complex mathematical concepts and problems in various fields of study.
Latest Posts
Latest Posts
-
30 Meters Is How Many Feet
Apr 09, 2025
-
Orbitals That Have The Same Energy Are Called
Apr 09, 2025
-
How Many Milliamps In One Amp
Apr 09, 2025
-
An Animal That Eats Another Animal Is Called
Apr 09, 2025
-
6 928 Rounded To The Nearest Tenth
Apr 09, 2025
Related Post
Thank you for visiting our website which covers about Which Number Is A Factor Of 51 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.