Calculating Ka From A Titration Curve
Juapaving
Apr 02, 2025 · 5 min read
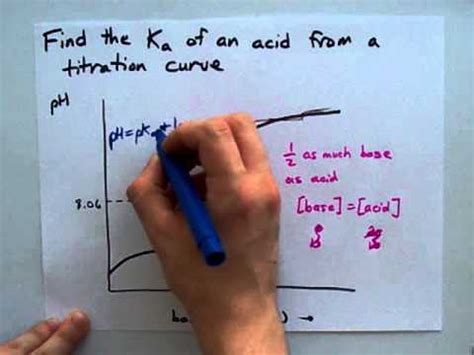
Table of Contents
Calculating Ka from a Titration Curve: A Comprehensive Guide
Determining the acid dissociation constant, Ka, is crucial in understanding the behavior of weak acids. While various methods exist, analyzing a titration curve offers a direct and insightful approach. This comprehensive guide will walk you through the process of calculating Ka from a titration curve, covering theoretical underpinnings, practical steps, and common pitfalls to avoid.
Understanding the Titration Curve and its Relationship to Ka
A titration curve graphically represents the change in pH of a solution as a strong base (or acid) is added. For a weak acid titrated with a strong base, the curve exhibits a characteristic gradual rise in pH initially, followed by a sharper increase near the equivalence point, and finally a gradual leveling off at higher pH values. The shape and specific points on this curve are directly related to the Ka of the weak acid.
Key Features of the Titration Curve:
-
Initial pH: The pH at the beginning of the titration reflects the initial concentration and Ka of the weak acid. A weaker acid (smaller Ka) will have a higher initial pH than a stronger acid (larger Ka) at the same concentration.
-
Half-Equivalence Point: This is the point where exactly half the volume of base required to reach the equivalence point has been added. At this crucial point, the concentration of the weak acid and its conjugate base are equal. Using the Henderson-Hasselbalch equation, we can directly determine the pKa (and thus Ka):
pH = pKa + log([A⁻]/[HA])
Since [A⁻] = [HA] at the half-equivalence point, log([A⁻]/[HA]) = 0, therefore:
pH = pKa
-
Equivalence Point: This is the point where the moles of added base are stoichiometrically equal to the moles of weak acid initially present. The pH at the equivalence point is not directly related to pKa but depends on the concentration of the conjugate base and its hydrolysis.
-
Buffer Region: The region of the curve surrounding the half-equivalence point is known as the buffer region. This region demonstrates the buffering capacity of the weak acid/conjugate base system. Small additions of base cause minimal pH changes due to the equilibrium between the acid and its conjugate base.
Step-by-Step Calculation of Ka from a Titration Curve
To calculate Ka, we'll primarily focus on the half-equivalence point:
1. Obtain the Titration Curve: This can be experimentally determined or obtained from literature or simulated data. The curve should clearly show the pH versus the volume of titrant added.
2. Identify the Half-Equivalence Point: Locate the volume of titrant added that is exactly half the volume required to reach the equivalence point. The equivalence point is typically identified by a sharp increase in pH.
3. Determine the pH at the Half-Equivalence Point: Find the pH value corresponding to the volume identified in step 2 on the titration curve.
4. Calculate the pKa: The pH at the half-equivalence point is equal to the pKa of the weak acid:
pKa = pH (at half-equivalence point)
5. Calculate the Ka: Use the following relationship to convert pKa to Ka:
Ka = 10⁻ᵖᵏᵃ
Illustrative Example
Let's consider a hypothetical titration of a weak acid, HA, with a strong base, NaOH. Suppose the titration curve shows that the equivalence point is reached at 25.0 mL of NaOH added. The half-equivalence point would therefore be at 12.5 mL of NaOH. If the pH at 12.5 mL is 4.75, then:
- pKa = 4.75
- Ka = 10⁻⁴·⁷⁵ ≈ 1.78 x 10⁻⁵
This example shows a straightforward calculation, ideal for showcasing the method. Real-world data might present more nuanced challenges.
Dealing with Real-World Data and Potential Complications
While the half-equivalence point method is convenient, several factors can influence the accuracy of Ka determination from a titration curve:
1. Inaccurate Equivalence Point Determination:
A poorly defined equivalence point due to a weak acid or a dilute solution can lead to significant error in pinpointing the half-equivalence point. Careful observation and potentially the use of derivative plots (plotting ΔpH/ΔV against volume) can help improve accuracy.
2. Activity Effects:
At high ionic strengths, activity coefficients deviate significantly from unity. This impacts the calculated Ka values as the concentration is not a true reflection of the effective concentration. Using activity instead of concentration corrects for this.
3. Multiple pKa Values:
Polyprotic acids (acids with multiple ionizable protons) will exhibit multiple equivalence points and buffer regions. Each pKa value will need to be determined separately by locating the corresponding half-equivalence point.
4. Experimental Errors:
Errors in volumetric measurements (pipetting, burette reading), pH meter calibration, or temperature fluctuations during the titration can introduce uncertainties in the results. Replicate measurements and careful experimental technique are essential to minimize error.
5. Non-ideal Behavior:
Some weak acids exhibit significant deviations from ideal behavior, particularly at high concentrations. This might necessitate the use of more sophisticated computational methods for accurate Ka determination.
Advanced Techniques for Ka Determination
For more complex situations or higher accuracy, more sophisticated methods can be employed:
-
Derivative Methods: Plotting the first or second derivative of the titration curve can provide a sharper indication of the equivalence point and half-equivalence point, leading to more accurate pKa determination.
-
Non-linear Regression: Fitting the titration data to theoretical models using non-linear regression analysis can provide a more robust and accurate estimation of the pKa, accounting for the effects mentioned above. This often requires specialized software.
Conclusion
Calculating Ka from a titration curve provides a practical and insightful method for determining the acidity of weak acids. While the half-equivalence point method offers a simplified approach, awareness of potential complications and the availability of advanced techniques are crucial for accurate and reliable results. By carefully considering experimental errors, activity effects, and the nature of the acid, researchers can obtain valuable information about the acid dissociation equilibrium and its implications. Mastering this technique equips scientists and students with a powerful tool for characterizing weak acids and understanding their behavior in various chemical systems. The importance of careful experimental procedure, accurate data analysis, and an understanding of potential error sources cannot be overstated. Remember, consistent and meticulous work is key to achieving reliable and meaningful results in acid-base chemistry.
Latest Posts
Latest Posts
-
1 Out Of 10 As A Percentage
Apr 03, 2025
-
How Are Prokaryotes And Eukaryotes Alike
Apr 03, 2025
-
Which Of The Following Statements Is Always True
Apr 03, 2025
-
Balanced Chemical Equation For Magnesium Oxide
Apr 03, 2025
-
What Is The Group Of Birds Called
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Calculating Ka From A Titration Curve . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
