Calculate Water Pressure From Tank Height
Juapaving
Mar 28, 2025 · 5 min read
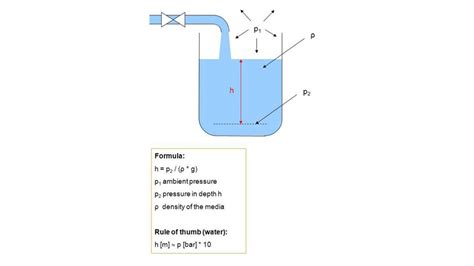
Table of Contents
Calculating Water Pressure from Tank Height: A Comprehensive Guide
Understanding how to calculate water pressure based on tank height is crucial in various applications, from designing irrigation systems and plumbing installations to ensuring the safety and efficiency of water towers and other elevated storage tanks. This comprehensive guide will delve into the principles behind this calculation, explore the relevant formulas, and discuss factors that can influence the results. We'll also consider practical examples and applications to solidify your understanding.
Understanding the Fundamentals: Pressure, Height, and Gravity
The pressure exerted by water at a given depth is fundamentally determined by the weight of the water column above it. This weight is a direct result of gravity acting on the water's mass. The higher the water column, the greater the weight, and consequently, the higher the pressure. This relationship is described by a simple, yet powerful, formula.
The Role of Gravity:
Gravity is the constant force pulling everything towards the earth's center. It's what gives water its weight, and this weight is responsible for the pressure exerted at the bottom of a water column (or at any point within it). The standard acceleration due to gravity (g) is approximately 9.81 m/s². While this value can vary slightly depending on location, it's a consistent enough approximation for most practical calculations.
Density of Water:
The density of water plays a significant role. While the density varies slightly with temperature and salinity, for most purposes, we can use a standard value of 1000 kg/m³. This value represents the mass of water per unit volume.
The Hydrostatic Pressure Formula
The cornerstone of calculating water pressure from tank height is the hydrostatic pressure formula:
P = ρgh
Where:
- P represents the pressure (typically measured in Pascals, Pa).
- ρ (rho) represents the density of water (1000 kg/m³).
- g represents the acceleration due to gravity (9.81 m/s²).
- h represents the height of the water column (measured in meters).
This formula neatly encapsulates the relationship between pressure, density, gravity, and height. It shows that pressure is directly proportional to the height of the water column: doubling the height doubles the pressure, assuming constant density and gravity.
Converting Units and Practical Applications
While the formula uses SI units (Pascals, kilograms, meters, and seconds), you might encounter different units in real-world applications. It's crucial to ensure consistent units throughout the calculation to obtain accurate results.
Common Unit Conversions:
- Pascals (Pa) to Kilopascals (kPa): Divide by 1000 (1 kPa = 1000 Pa)
- Pascals (Pa) to Bars: Divide by 100,000 (1 bar = 100,000 Pa)
- Pascals (Pa) to Pounds per square inch (psi): Multiply by 0.000145 (1 psi ≈ 6895 Pa)
- Meters (m) to Feet (ft): Multiply by 3.281
Practical Examples:
Example 1: Simple Water Tower Calculation
Let's say we have a water tower with a water level 20 meters above a tap. What is the water pressure at the tap?
Using the formula:
P = ρgh = (1000 kg/m³)(9.81 m/s²)(20 m) = 196,200 Pa = 196.2 kPa
This translates to approximately 28.4 psi.
Example 2: Irrigation System Design
Suppose you're designing an irrigation system and need to determine the pressure at the end of a pipe 50 feet below a water tank.
First, convert feet to meters: 50 ft * 0.3048 m/ft ≈ 15.24 m
Then apply the formula:
P = ρgh = (1000 kg/m³)(9.81 m/s²)(15.24 m) ≈ 149,452 Pa ≈ 149.5 kPa
This is approximately 21.7 psi.
Example 3: Considering Pressure Loss in Pipes
In real-world scenarios, you need to account for friction losses within pipes. These losses reduce the actual pressure at the point of use. The Darcy-Weisbach equation or other methods are employed to calculate these head losses. The pressure calculated using the hydrostatic pressure formula represents the theoretical maximum pressure; the actual pressure will be lower due to friction.
Factors Influencing Water Pressure
While the hydrostatic pressure formula provides a solid foundation, several factors can influence the actual water pressure:
Water Temperature:
As water temperature increases, its density decreases slightly. This, in turn, results in a minor reduction in pressure. However, this effect is generally negligible for most practical purposes unless dealing with significant temperature variations.
Pipe Diameter and Length:
As mentioned, friction within pipes reduces pressure. The longer and narrower the pipe, the greater the friction loss. This is why proper pipe sizing is essential for efficient water distribution systems.
Pipe Material:
The roughness of the pipe's inner surface affects friction. Smoother pipes generally lead to lower pressure losses.
Minor Losses:
Fittings such as elbows, valves, and tees create additional pressure losses due to changes in flow direction and velocity.
Advanced Considerations: Variations in Gravity and Density
While we've used standard values for gravity and water density, these values can vary slightly based on location and water composition. For high-precision calculations, it's essential to consider these variations:
Variations in Gravity:
Gravity is not perfectly uniform across the Earth's surface. Altitude and latitude affect the gravitational acceleration, albeit minimally for most applications. Highly accurate calculations might require using a locally measured value of g.
Variations in Water Density:
The density of water changes with temperature and salinity. Seawater, for example, has a higher density than freshwater. When dealing with non-freshwater, using the appropriate density value is crucial for accurate pressure calculations.
Conclusion: Accurate Pressure Calculation for Diverse Applications
Calculating water pressure from tank height is a fundamental concept with wide-ranging applications. While the hydrostatic pressure formula (P = ρgh) provides a simple yet effective starting point, understanding the influencing factors and employing appropriate unit conversions ensures accurate results. Remember to always consider friction losses in pipes and fittings for real-world scenarios. This detailed guide provides a solid foundation for those working with water systems, enabling informed decisions and efficient design practices. From simple home plumbing to complex industrial applications, grasping the principles behind hydrostatic pressure is key to success.
Latest Posts
Latest Posts
-
How Many Lines Of Symmetry Are In A Star
Mar 31, 2025
-
Which Of The Following Is An Ecosystem
Mar 31, 2025
-
Least Common Multiple Of 20 And 50
Mar 31, 2025
-
List The Factors Of 100 That Are Prime
Mar 31, 2025
-
Do The Diagonals Of A Kite Bisect Teachother
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Calculate Water Pressure From Tank Height . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
