How Many Lines Of Symmetry Are In A Star
Juapaving
Mar 31, 2025 · 5 min read
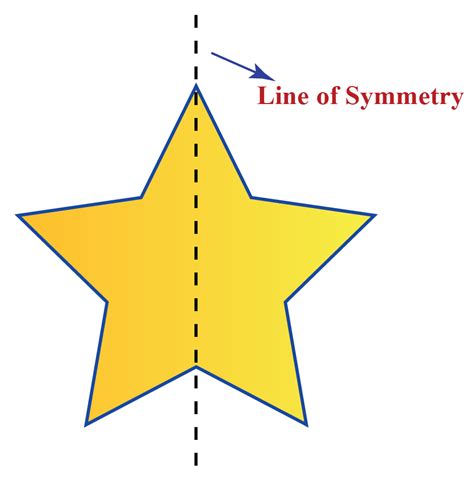
Table of Contents
How Many Lines of Symmetry Does a Star Have? A Deep Dive into Geometry
The seemingly simple question, "How many lines of symmetry does a star have?" opens a fascinating exploration into geometry, specifically the properties of regular polygons and their stellations. The answer, however, isn't a straightforward single number, but depends entirely on the type of star you're considering. This article delves into the mathematics behind lines of symmetry, explores different types of stars, and provides a comprehensive guide to determining the number of lines of symmetry for various star shapes.
Understanding Lines of Symmetry
Before we tackle stars, let's establish a firm understanding of lines of symmetry. A line of symmetry, also known as a line of reflection, divides a shape into two identical halves that are mirror images of each other. If you were to fold the shape along the line of symmetry, both halves would perfectly overlap. Not all shapes possess lines of symmetry; some have many, while others have none at all.
Identifying Lines of Symmetry in Simple Shapes
Consider a simple square. It has four lines of symmetry: two that run horizontally and vertically through the center, and two that run diagonally from corner to corner. A circle, on the other hand, has an infinite number of lines of symmetry, as any line passing through its center will divide it into two identical halves. A regular hexagon boasts six lines of symmetry – three connecting opposite vertices and three bisecting opposite sides.
The Complexity of Star Shapes
Stars, unlike simple polygons, present a more complex scenario. The number of lines of symmetry in a star is directly related to its construction, specifically the number of points and the way those points are connected. A "star" can refer to a wide variety of shapes, leading to diverse results.
Regular Stars and Their Symmetry
A regular star is a polygon created by connecting non-adjacent vertices of a regular polygon. The most commonly recognized star, the five-pointed star (pentagram), is a prime example. The number of points in a regular star significantly influences its symmetry.
The Five-Pointed Star (Pentagram)
The five-pointed star, perhaps the most ubiquitous star shape, possesses five lines of symmetry. These lines run from each point to the midpoint of the opposite edge. Notice that these lines are not only lines of reflection but also lines of rotational symmetry, meaning the star can be rotated around its center by 72 degrees (360/5) and still appear unchanged.
The Six-Pointed Star (Hexagram)
The six-pointed star, often associated with Judaism and other cultures, has a different symmetry pattern. This is often misidentified as a star; it's actually a combination of two equilateral triangles. The hexagram possesses six lines of symmetry: three lines connecting opposite vertices and three bisecting opposite sides. It's important to distinguish this from a true six-pointed star formed by connecting non-adjacent vertices of a hexagon.
Stars with More Points
As the number of points in a regular star increases, the number of lines of symmetry also changes. A seven-pointed star will have seven lines of symmetry, an eight-pointed star eight, and so on, following a pattern where the number of points equals the number of lines of symmetry for a regular star. However, it's crucial to understand that the construction of these stars – the specific way the vertices are connected – significantly affects the symmetry.
Irregular Stars and Symmetry
Not all stars are regular. Irregular stars, those with points that are not equally spaced or connected in a uniform manner, can have a variable number of lines of symmetry, or even none at all. The symmetry of an irregular star depends entirely on its specific shape and configuration. It’s often difficult to determine the lines of symmetry without using geometric software or tools.
Factors Affecting Symmetry in Irregular Stars
The following aspects play a crucial role in determining the lines of symmetry for irregular stars:
- Point Distribution: If the points are not evenly spaced, the chances of having multiple lines of symmetry decrease drastically.
- Connection Pattern: The way the points are connected dictates the shape’s overall symmetry. Random connections generally result in a lack of symmetry.
- Edge Lengths: Unequal edge lengths further contribute to asymmetrical structures.
For irregular stars, visually inspecting the figure is often the best approach to identifying lines of symmetry, if any exist.
Mathematical Approaches to Determining Symmetry
For complex stars or those with a large number of points, mathematical methods can be more efficient. However, these methods often require advanced mathematical concepts beyond the scope of a general audience. These include group theory and concepts relating to rotational symmetry.
Software and computational geometry tools can provide significant assistance in identifying and visualizing lines of symmetry for stars of all complexities. Many free or commercial geometric software packages can calculate and visually display the lines of symmetry of any given polygon, including stars.
Real-World Applications of Star Symmetry
Understanding the symmetry of stars extends beyond the realm of abstract mathematics. The principles of symmetry have various applications in different fields:
- Design: Symmetrical star shapes are frequently used in logos, artwork, and architectural design for their aesthetically pleasing qualities.
- Nature: While perfect geometric stars are rare in nature, certain natural phenomena, such as some crystalline structures, exhibit star-like shapes with varying degrees of symmetry.
- Engineering: Symmetry plays a critical role in engineering design, impacting structural stability and performance.
Conclusion: A Star's Symmetry – More Than Meets the Eye
The seemingly simple question about the number of lines of symmetry in a star reveals the multifaceted nature of geometric shapes and the subtle interplay of mathematical principles. While regular stars exhibit straightforward symmetry patterns where the number of points typically equals the number of lines of symmetry, irregular stars often possess fewer lines of symmetry or none at all. Understanding these differences requires a close examination of the star's construction and properties. This exploration demonstrates that seemingly simple shapes can hold a surprising depth of mathematical intricacy, highlighting the beauty and complexity of geometry in the world around us. Using the knowledge gained here, you can now confidently approach any star shape and determine its lines of symmetry, furthering your understanding of the fundamental concepts of geometry.
Latest Posts
Latest Posts
-
A Chemical Equation Is Balanced When
Apr 01, 2025
-
Cold B Lood Vs Cold Heart
Apr 01, 2025
-
Lowest Common Denominator Of 12 And 9
Apr 01, 2025
-
What Is The Advantage Of A Four Chambered Heart
Apr 01, 2025
-
Endocrine Glands Are Often Called Ducted Glands True False
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about How Many Lines Of Symmetry Are In A Star . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
