Abc And Cd Intersect At Point O As Shown Below
Juapaving
Mar 26, 2025 · 5 min read
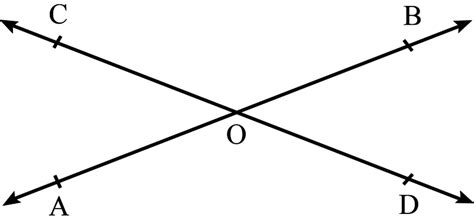
Table of Contents
ABC and CD Intersect at Point O: A Comprehensive Exploration of Geometric Relationships
This article delves into the geometric relationships formed when two lines, AB and CD, intersect at a point O. We'll explore various concepts, theorems, and applications stemming from this fundamental intersection, enriching your understanding of geometry and its practical implications. This detailed examination will cover aspects relevant for students, educators, and anyone interested in deepening their geometric knowledge.
Understanding the Basic Intersection
When two lines intersect, they form several key geometric features. The most fundamental is the point of intersection itself, denoted as O in our case. This point is crucial because it's the origin for various angles and relationships. The lines AB and CD create four angles around point O. These angles possess specific relationships that are the subject of much geometric study.
Defining the Angles
We can label the angles formed by the intersection as follows:
- ∠AOD: The angle formed by rays OA and OD.
- ∠AOC: The angle formed by rays OA and OC.
- ∠BOC: The angle formed by rays OB and OC.
- ∠BOD: The angle formed by rays OB and OD.
Understanding the relationships between these angles is key to solving many geometric problems.
Exploring Angle Relationships
The angles formed by intersecting lines AB and CD are not arbitrary; they exhibit specific relationships. These relationships are crucial for problem-solving and further geometric understanding.
Vertically Opposite Angles
Vertically opposite angles are angles that are opposite each other when two lines intersect. In our scenario:
- ∠AOD and ∠BOC are vertically opposite angles.
- ∠AOC and ∠BOD are vertically opposite angles.
A fundamental theorem in geometry states that vertically opposite angles are always equal. This means:
- ∠AOD = ∠BOC
- ∠AOC = ∠BOD
This theorem is essential for solving numerous geometric problems involving intersecting lines. It simplifies calculations and allows for the deduction of unknown angle measures based on known ones.
Linear Pairs
A linear pair consists of two adjacent angles formed by intersecting lines that are supplementary; their sum equals 180 degrees. In our diagram:
- ∠AOD and ∠AOC form a linear pair.
- ∠AOC and ∠BOC form a linear pair.
- ∠BOC and ∠BOD form a linear pair.
- ∠BOD and ∠AOD form a linear pair.
Therefore:
- ∠AOD + ∠AOC = 180°
- ∠AOC + ∠BOC = 180°
- ∠BOC + ∠BOD = 180°
- ∠BOD + ∠AOD = 180°
Understanding linear pairs is crucial for solving problems where one angle is known, and the adjacent angle needs to be determined. The supplementary relationship allows for easy calculation.
Applications and Extensions
The intersection of lines AB and CD at point O is not merely a theoretical concept; it has far-reaching applications in various fields.
Solving Geometric Problems
The relationships between angles formed by intersecting lines are frequently used to solve problems in geometry. For example, given the measure of one angle, we can deduce the measures of the other three angles using the principles of vertically opposite angles and linear pairs.
Example: If ∠AOD = 70°, then ∠BOC = 70° (vertically opposite angles), ∠AOC = 180° - 70° = 110°, and ∠BOD = 110° (linear pairs).
Coordinate Geometry
In coordinate geometry, the intersection point O can be determined algebraically by finding the point where the equations of lines AB and CD intersect. This point provides valuable information about the lines' relative positions and properties.
Real-World Applications
The concepts of intersecting lines and their angle relationships have practical applications in various fields:
- Construction and Engineering: Understanding angles is crucial for building structures, designing roads, and creating other infrastructure.
- Computer Graphics: Intersections of lines are fundamental in computer graphics for rendering images and creating realistic simulations.
- Navigation: Understanding angles is essential for navigation, particularly in aviation and maritime applications.
- Surveying: Accurate measurements of angles are fundamental in surveying for land measurement and mapping.
Advanced Concepts and Further Exploration
The intersection of lines AB and CD at point O opens the door to more advanced geometric concepts:
Perpendicular Lines
If lines AB and CD intersect at a right angle (90°), they are considered perpendicular. In this case, all four angles formed at the intersection are equal to 90°. This simplifies many geometric calculations and is a frequent feature in construction and design.
Angle Bisectors
An angle bisector divides an angle into two equal halves. If we were to draw an angle bisector for each of the four angles formed at point O, we would create further relationships and symmetries within the diagram. This concept is crucial for understanding more complex geometric structures.
Concurrent Lines
If multiple lines intersect at a single point, they are considered concurrent. Point O could be the point of concurrency for more than two lines, leading to more complex angle relationships and geometrical configurations.
Conclusion: A Foundation for Further Geometric Understanding
The seemingly simple intersection of lines AB and CD at point O provides a rich foundation for understanding numerous geometric concepts and their applications. By mastering the relationships between vertically opposite angles and linear pairs, you unlock the ability to solve a wide range of geometric problems and appreciate the underlying structure of shapes and spaces. This understanding extends beyond theoretical geometry, finding practical applications in various fields, highlighting the importance of these fundamental geometric principles. Further exploration into advanced concepts like perpendicular lines, angle bisectors, and concurrent lines will deepen your understanding of this core geometric relationship and its implications. The exploration of this simple intersection reveals the interconnectedness and elegance inherent in the study of geometry.
Latest Posts
Latest Posts
-
How Many Hours Are In 90 Minutes
Mar 29, 2025
-
What Is 40 Percent Of 60
Mar 29, 2025
-
How Much Atp Does The Etc Produce
Mar 29, 2025
-
What Is 1 2 Of 1 Percent
Mar 29, 2025
-
What Is The Gcf Of 18 And 12
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about Abc And Cd Intersect At Point O As Shown Below . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
