What Is The Gcf Of 18 And 12
Juapaving
Mar 29, 2025 · 5 min read
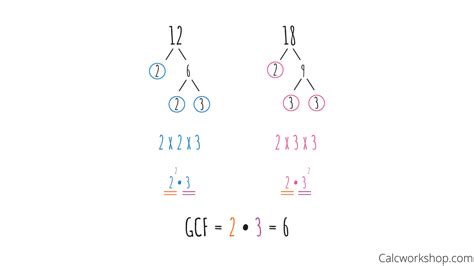
Table of Contents
What is the GCF of 18 and 12? A Deep Dive into Greatest Common Factors
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the process and its applications reveals a surprisingly rich mathematical concept with practical uses far beyond the classroom. This article will not only answer the question, "What is the GCF of 18 and 12?", but will explore the various methods for finding the GCF, delve into its significance in mathematics, and demonstrate its real-world applications.
Understanding Greatest Common Factors (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes evenly into both numbers. For example, if we consider the numbers 12 and 18, we're looking for the largest number that perfectly divides both.
Let's start with our core question: What is the GCF of 18 and 12?
Methods for Finding the GCF of 18 and 12
Several methods can efficiently determine the GCF, each offering a different perspective on the underlying mathematical principles. Let's explore three common approaches:
1. Listing Factors
This is the most straightforward method, particularly useful for smaller numbers. We list all the factors of each number and then identify the largest factor common to both.
- Factors of 12: 1, 2, 3, 4, 6, 12
- Factors of 18: 1, 2, 3, 6, 9, 18
Comparing the lists, we see that the common factors are 1, 2, 3, and 6. The greatest of these common factors is 6. Therefore, the GCF of 18 and 12 is 6.
2. Prime Factorization
This method utilizes the fundamental theorem of arithmetic, which states that every integer greater than 1 can be uniquely represented as a product of prime numbers (numbers divisible only by 1 and themselves). By breaking down each number into its prime factors, we can easily identify the common factors.
- Prime factorization of 12: 2 x 2 x 3 = 2² x 3
- Prime factorization of 18: 2 x 3 x 3 = 2 x 3²
Now, we identify the common prime factors and their lowest powers: Both numbers share a single '2' and a single '3'. Multiplying these common prime factors together gives us 2 x 3 = 6. Thus, the GCF of 18 and 12 is 6. This method is particularly efficient for larger numbers.
3. Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the GCF of two numbers, especially when dealing with larger integers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 18 and 12:
- 18 > 12: Subtract the smaller number from the larger: 18 - 12 = 6
- Now consider the numbers 12 and 6.
- 12 > 6: Subtract: 12 - 6 = 6
- Now we have 6 and 6. Since the numbers are equal, the GCF is 6.
The Euclidean algorithm provides a systematic and efficient way to find the GCF, even for very large numbers where listing factors or prime factorization becomes cumbersome.
Significance of GCF in Mathematics
The GCF is a fundamental concept in number theory and has numerous applications within mathematics and beyond:
-
Simplifying Fractions: The GCF is crucial for simplifying fractions to their lowest terms. For instance, the fraction 12/18 can be simplified by dividing both the numerator and denominator by their GCF (6), resulting in the equivalent fraction 2/3.
-
Solving Diophantine Equations: These equations involve finding integer solutions. The GCF plays a vital role in determining the existence and nature of these solutions.
-
Modular Arithmetic: The concept of GCF is central to modular arithmetic, a system of arithmetic for integers, where numbers "wrap around" upon reaching a certain value (the modulus). GCF helps determine properties of modular arithmetic operations.
-
Abstract Algebra: GCF extends its significance into abstract algebra, where it's related to concepts like ideals and greatest common divisors in rings.
Real-World Applications of GCF
While the theoretical applications are significant, the GCF has numerous practical real-world uses:
-
Dividing Objects Equally: Imagine you have 18 apples and 12 oranges, and you want to distribute them into identical bags, with the same number of apples and oranges in each bag. The GCF (6) tells you can make 6 bags, each with 3 apples and 2 oranges.
-
Construction and Design: Architects and engineers use GCF to determine the largest common divisor of measurements when designing structures or layouts. This ensures efficient and harmonious proportions.
-
Music Theory: In music, the GCF is used to find the greatest common divisor of note durations, which is important for rhythm and harmony.
-
Computer Science: GCF algorithms are utilized in various computer science applications, including cryptography and data compression, for tasks such as finding the greatest common divisor of two polynomials.
-
Scheduling and Planning: Determining the optimal time interval for recurring events, such as meetings or production cycles, often relies on finding the greatest common divisor of different time periods.
Beyond the Basics: Exploring Related Concepts
Understanding the GCF often leads to exploring related mathematical concepts:
-
Least Common Multiple (LCM): The LCM is the smallest positive integer that is a multiple of each of the integers. The GCF and LCM are related through the formula: GCF(a, b) x LCM(a, b) = a x b
-
Modular Inverse: In modular arithmetic, the modular inverse of a number a modulo n exists only if a and n are coprime (their GCF is 1). This concept is essential in cryptography.
Conclusion: The Power of a Simple Concept
The seemingly simple question, "What is the GCF of 18 and 12?" opens the door to a wide range of mathematical concepts and real-world applications. From simplifying fractions to solving complex equations and designing efficient systems, the GCF serves as a fundamental building block in various fields. Understanding the different methods for calculating the GCF and appreciating its significance underscores the power and elegance of basic mathematical principles. By mastering this fundamental concept, you enhance your problem-solving abilities and expand your understanding of the interconnectedness of mathematics. So, remember the GCF isn't just about finding the largest common factor; it's about understanding the underlying structure and beauty of numbers and their relationships.
Latest Posts
Latest Posts
-
What Is The Least Common Multiple Of 12 And 15
Apr 01, 2025
-
Carbon Dioxide And Water Combine To Form
Apr 01, 2025
-
What Is Lcm Of 3 And 8
Apr 01, 2025
-
What Is The Lcm Of 9 12 15
Apr 01, 2025
-
Five Letter Word Ends With Er
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 18 And 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
